
Épreuve sur les notions d’angle solide, de source lumineuse et de champ vectoriel.
– Champ : primitives et directives graphiques, champs vectoriels.
– Documents autorisés : zone personnelle, Internet, site OWL, Hypatie.
– Lundi 26 mars 2007, CECNB, A1-A2, 95 min.
– Moyenne de classe : 3.47
– Écart type : 0.74
– Effectif : N=17
1. Angle solide
- Exprimez l’angle au sommet θ d’un cône circulaire en fonction de son rayon r et de sa demi-hauteur h.
- Exprimez l’angle solide Ω découpé par un cône circulaire d’angle au sommet θ.
- Calculez la demi-hauteur h d’un cône circulaire de rayon r=1 unité qui découpe dans l’espace un angle solide d’un stéradian.
- Calculez l’aire délimitée par ce cône sur une sphère de rayon
unité lorsque le sommet du cône se trouve au centre de la sphère. - Dessinez ce cône.
- Dessinez la figure suivante :
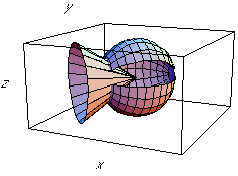
2. Sources lumineuses
- Placez trois points colorés aux endroits indiqués (voir figure).
- Animez ces points en leur faisant décrire des cercles dans le plan xz.
- Donnez les positions initiales des sources lumineuses (rouge, verte et bleue) représentées par ces points.
- Animez ces sources pour produire l’éclairage observé.
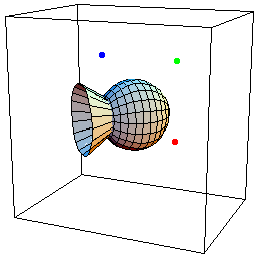
3. Champ vectoriel
Un champ vectoriel est donné par :
- m(x, y)=0.5(x + y) - 1
- n(x, y)=0.5(x - 0.2y2)
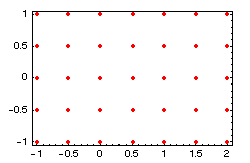
- Dessinez ces points.
- Dessiner les vecteurs de ce champ associés aux points ci-dessus.
- Dessinez dans cette région de l’espace une courbe définie par x(t)=acos(ωt) et y(t)=bsin(ωt) avec a=2, b=1 et ω=2π.
- Dessinez les vecteurs associés à une vingtaine de points de cette courbe.
– Points par problème et par question
| item | points |
|---|---|
| θ=f(r, h) | 2/2 |
| Ω=f(θ) | 2/2 |
| h | 2/2 |
| Aire | 2/2 |
| Cône | 2/2 |
| Figure | 4/4 |
| Total | 14/14 |
| item | points |
|---|---|
| Points (position, couleur) | 3/3 |
| Points (animation) | 4/4 |
| Sources (position, couleur) | 3/3 |
| Animation de l’éclairage | 4/4 |
| Total | 14/14 |
| item | points |
|---|---|
| Dessin des points | 2/2 |
| Dessin des vecteurs | 4/4 |
| Dessin de la courbe | 4/4 |
| Vecteurs sur la courbe | 4/4 |
| Total | 14/14 |
– Barème
Corrigé
Angle solide
1. L’angle au sommet θ d’un cône de rayon r et de hauteur 2h est donné par :
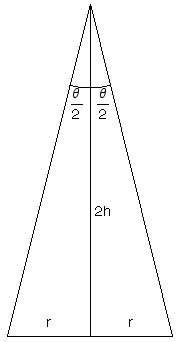
2. L’angle solide Ω découpé par un cône circulaire d’angle au sommet θ est donné par :
Vous pouviez trouver cette expression dans la définition du stéradian donnée ici.
3. On obtient la demi-hauteur h d’un cône circulaire de rayon r=1 qui découpe dans l’espace un angle solide d’un stéradian en résolvant l’équation suivante par rapport à h :
On trouve $h=\frac2\pi - 12\sqrt4\pi -1$
4. L’aire délimitée par ce cône sur une sphère de rayon 1 est égale à 1 (c’est la définition même du stéradian que vous pouviez trouver ici).
5. Pour obtenir la figure, il faut faire subir une translation -h selon l’axe z au cône de hauteur 2h, puis faire subir à la figure résultante une rotation de $\frac\pi2$ selon $\theta$ et de $\frac\pi4$ selon $\psi$ (angles d’Euler).
Sources lumineuses
Les trois points doivent se trouver dans le plan xz. Leur coordonnée y est donc constante. Pour trouver la position des sources, vous pouviez utiliser la correspondance établie au cours et donnée sous animation dans le résumé du 5 mars. Le code détaillé de cette animation pouvait être copié et adapté à votre problème.
L’animation s’obtient à l’aide d’un Table permettant de faire varier les coordonnées x et z des points dans le système de repérage de la figure et xs et ys dans le système de repérage des sources.
Champ vectoriel
Le dessin des flèches fait appel au module Arrow. Les courbes fermées s’obtiennent à l’aide de ParametricPlot.
– Points de l’espace où l’on examine le champ vectoriel :
– Définition du champ et dessin des vecteurs aux points considérés :
– Définition d’une courbe fermée dans le champ :
– Dessin de vecteurs du champ associés à des points de la courbe :
