Tableau des notions et des activités

Présentation

Pour transvaser un liquide d’un récipient dans un autre, on plonge un tube de verre verticalement dans le liquide jusqu’au fond du premier récipient rempli. On laisse pénétrer le liquide à l’intérieur du tube puis on ferme l’orifice supérieur du tube. On déplace ensuite le tube au-dessus de l’autre récipient et on libère l’orifice, laissant ainsi le liquide s’échapper du tube et tomber dans le second récipient.

Objectifs
– prendre conscience des limites de l’usage des proportions
– établir un graphique
– modéliser un phénomène (extension)
– simuler une évolution (extension)

Notions
– pression
– proportionnalité
– processus discret
– modèle

Matériel
– 2 cylindres gradués (100 ml)
– 2 erlenmeyers (200 ml)
– 1 tube de verre cylindrique (25-30 cm)
– 1 pied à coulisse
– 1 ordinateur (pour l’extension)

Durée
– 2 fois 45 minutes

Activités

1. Transvasez la moitié du contenu du récipient plein dans le récipient vide en comptant le nombre d’opérations effectuées et en relevant le niveau dans chaque récipient toutes les 2 opérations.
2. Estimez le nombre d’opérations nécessaires pour transvaser 3/4 du liquide. Notez ce nombre, réalisez ce transfert et comparez le résultat à votre pronostic.
3. Estimez maintenant le nombre d’opérations nécessaires pour revenir à égalité de niveaux dans les deux récipients. Notez ce nombre, réalisez ce transfert et comparez le résultat à votre pronostic.
4. Esquissez l’allure de l’évolution du niveau dans chaque récipient en fonction du nombre d’opérations pour les trois transferts effectués.
5. Établissez pour chacun de ces transferts, un graphique (sur le même système d’axes) donnant le niveau en fonction du nombre d’opérations.
6. Comparez ces graphiques à l’allure esquissée pour chacun d’eux

Questions

1. Pourquoi le liquide reste-t-il dans le tube lors du déplacement d’un récipient à l’autre ?
2. Pourquoi le liquide s’échappe-t-il du tube lorsqu’on libère l’orifice ?
3. La quantité de liquide contenue dans le tube lors des déplacements d’un récipient à l’autre reste-t-elle la même durant tout le transvasement ?
4. De quoi la quantité de liquide contenue dans le tube dépend-elle ?
5. Le nombre d’opérations est-il modifié si on transfère les mêmes quantités entre erlenmeyer plutôt qu’entre cylindres ?

Extension

1. Construisez une représentation schématique de la description faisant apparaître :

• les grandeurs et paramètres retenus
• les relations entre ces éléments.

2. Formulez explicitement les relations entre les différents éléments.
3. Exprimez l’évolution des niveaux en utilisant les grandeurs mesurées.
4. Mesurez les grandeurs permettant de calculer l’évolution du niveau en fonction du nombre d’opérations.
5. Comparez les graphiques donnant les évolutions calculées et mesurées.
6. Interprétez les grandeurs du modèle (en les renommant) pour rendre compte de la notion de vitesse de réaction.

A l’attention du maître

1. Les grandeurs et paramètres retenus sont les suivants :

• volume initial de liquide dans le récipient
• volume transvasé par opération
• diamètre intérieur du récipient
• diamètre et épaisseur du tube (paramètres)

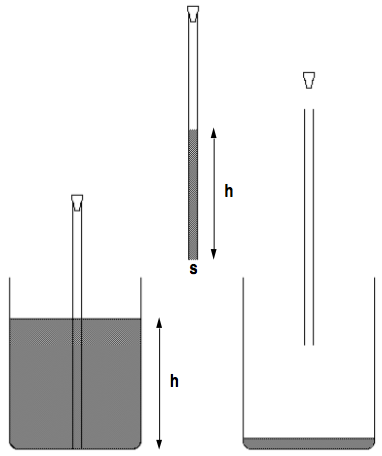
2. Le volume transvasé par opération est proportionnel à la hauteur h du niveau. Nous faisons l’hypothèse que les réservoirs sont des prismes droits et que l’épaisseur de la paroi du tube est négligeable. Pour une hauteur h et un rayon intérieur r du tube, le volume transvasé par opération vaut :

N. B. Pour un cylindre gradué, la hauteur h du niveau s’exprime à partir du rayon intérieur R du cylindre et du volume V de liquide qu’il contient :

3. L’évolution du volume V en fonction du nombre n d’opérations s’obtient en résolvant l’équation différentielle exprimant la proportionnalité entre le volume transvasé et la hauteur h(n) du niveau :

La solution est :

Code Mathematica permettant de résoudre l’équation exprimée à l’aide des grandeurs mesurées (diamètres au lieu des rayons) :

4. Exemple de valeurs mesurées :

• diamètre intérieur du cylindre : 2.700 ± 0.01 cm
• diamètre intérieur du tube : 0.580 ± 0.01 cm
• épaisseur du tube : 0.100 ± 0.01 cm

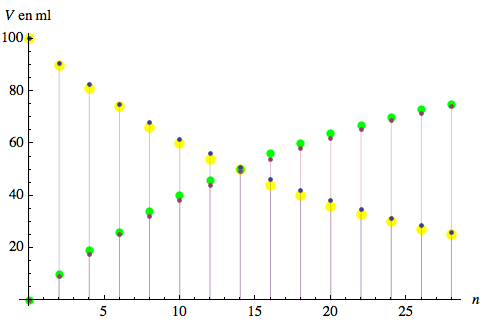
5. Le modèle peut être interprété et utilisé pour simuler une réaction chimique du type A$$$\longrightarrow$B. Les volumes correspondent alors à des nombres de moles, le volume transvasé à une vitesse de réaction et la section du tube à une constante cinétique.

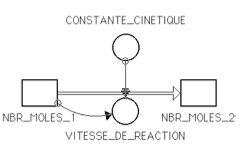
En remplaçant le flux par un biflux et en introduisant une deuxième constante cinétique, le modèle se généralise et permet d’interpréter des réactions chimiques du type A$\longleftrightarrow $B.