En travaillant avec des unités homogènes (temps mesuré en mètre), l’expression de l’énergie relativiste se simplifie et toutes les grandeurs qu’elle relie s’expriment dans la même unité (par exemple le kg ou le MeV).
par bernard.vuilleumier
Point de départ
La grande force de la relativité restreinte d’Einstein c’est de reposer sur un très petit nombre de principes. En postulant que la vitesse de la lumière est constante et qu’elle conserve la même valeur dans tous les référentiels inertiels, on parvient à déduire l’expression de l’énergie relativiste ainsi que la relation entre cette énergie et la quantité de mouvement d’un photon.
Invariance de l’intervalle
Considérons une émission lumineuse ponctuelle (éclatement d’une étincelle). La lumière émise forme un front d’onde sphérique qui se déplace à la vitesse constante c. Après un temps ts exprimé en seconde, le rayon de cette sphère vaudra $c^2 t_s^2=x^2+y^2+z^2$. À une dimension, cela donne $c^2 t_s^2=x^2$. Définissons l’intervalle I en posant $I={\sqrt{c^2 t_s^2-x^2}}$. [1]
Unités homogènes
Comme la vitesse de la lumière est constante, nous pouvons exprimer le temps t en mètre : un mètre de temps correspond alors au temps t mis par la lumière pour franchir un mètre. Le temps t exprimé en m est donc relié au temps ts exprimé en seconde par la relation t = cts. Lorsque le temps est exprimé dans les mêmes unités que la longueur – en mètre – l’intervalle devient
$I=\sqrt{t^2-x^2}$. Avec ces unités, ${\frac{dx}{dt}}$ qui correspond à la vitesse du photon est sans dimension et vaut 1.
Horaire d’un photon
L’horaire d’un photon (diagramme d’espace temps) se représente conventionnellement ainsi en relativité restreinte [2] :
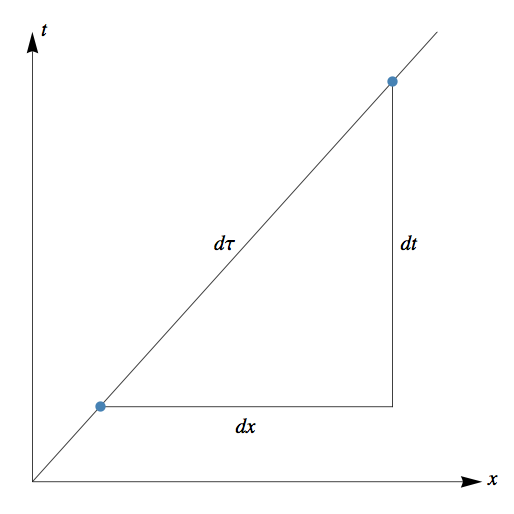
En multipliant la définition de l’intervalle par m on peut écrire :
${(mdt)}^2-{(mdx)}^2=0$
puis en divisant par $d\tau^2$
$(m\frac{dt}{d\tau})^2-(m\frac{dx}{d\tau})=0$
En posant $E={m\frac{dt}{d\tau}}$ pour l’énergie et $p={m\frac{dx}{d\tau}}$ pour la quantité de mouvement, on obtient l’expression reliant l’énergie du photon à sa quantité de mouvement. Pour un intervalle I > 0 (de type « temps ») m ne s’annule pas :
${\sqrt{E^2-p^2}}=0$
Dans cette expression, l’énergie et la quantité de mouvement sont exprimées dans la même unité. Pour obtenir l’expression donnant des joules, il faut multiplier chaque terme par c2.
