par Marco Moggiani, Masami Sarumaru
Dans ce laboratoire nous étudierons la relation fondamentale entre les trois plus importantes grandeurs électriques : celles-ci sont l’intensité du courant, la tension et enfin la résistance.
Nous vérifierons la véridicité de cette loi en faisant usage d’un ordinateur et d’une sonde de courant et de tension.

Objectifs :
– Déterminer la relation mathématique entre l’intensité du courant, la différence de potentiel et la résistance dans un circuit simple.
– Comparer le comportement d’une résistance à celui d’une ampoule électrique.
Questions préalables :
– En doublant la tension l’on remarque que le courant double nous faisant constater un lien entre ces deux grandeurs.
– La relation entre la tension et le courant est U=RI ; où U est égal à la tension, R à la résistance et I à l’intensité. Cela évolue selon une droite linéaire, c’est donc une relation proportionnelle.
Analyse :
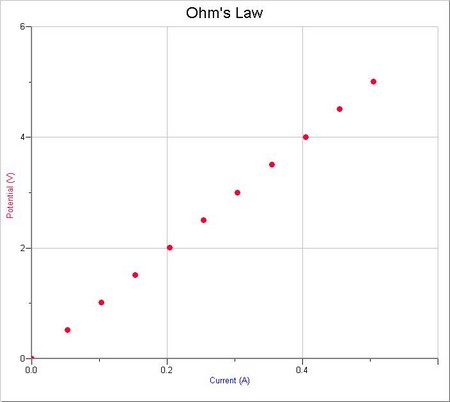
1. Dans ces deux exemples l’on a bien vérifié que les données initiales obtenues sont très proches de l’origine, l’on peut dire que la formule U=RI est donc respectée.
2. Pour la comparaison entre la valeur des constantes et les valeurs obtenues, l’on constate que les deux valeurs sont très proches de la valeur déclarée des deux résistances.
Respectivement 9.919 de pente pour la résistance de 10 ohms et 47.44 de pente pour la résistance à 47 ohms.
3. En vérifiant le code colorimétrique apposé sur les résistances l’on a trouvé une marge admise de 5% d’erreur.
Pour la résistance de 10 ohms cela donne théoriquement 0.5 ohms de marge d’erreur, et pour la résistance de 47 ohms, l’on trouve environ 2.35 ohms de marge d’erreur théorique calculée.
Pour ce qui en est de la vérification expérimentale :
pour la résistance de 10 ohms l’on se trouve dans le seuil de tolérance avec une différence de moins d’un dixième, la valeur admise est aussi respectée pour la résistance de 47 ohms où la précision obtenue est moins du demi ohm.
L’on a pu donc constater que la marge admise est respectée. La finesse des mesures nous a permis d’atteindre une précision élevée, nous permettant d’obtenir des valeurs compatibles avec la tolérance admise.
4. Les graphiques indiquent une relation linéaire entre la tension et l’intensité, nous pouvons donc en déduire une proportionnalité entre ces deux grandeurs. Nos mesures sont en accord avec la loi d’ohm.
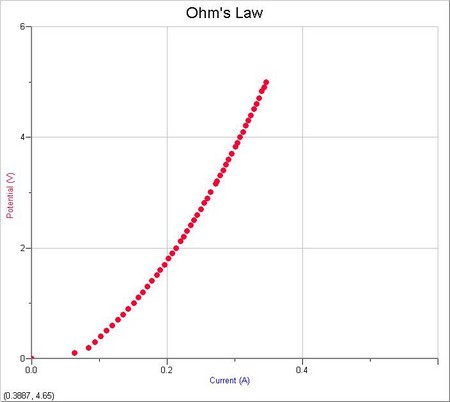
5. Pour les deux ampoules, la température du filament augmente la résistance, ce qui a comme influence de faire varier la pente de la droite au début et à la fin, principalement dans les zones de forte variation de température.
Plus la température augmente et plus la résistance augmente.
Voici la relation qui montre la variation de la résistance en fonction de la température :
R = r0 + r0 * a * deltaT
Où ro est la température initiale de R, a est le coefficient dépendant du matériau utilisé et T est la variation de la température.
6. Comme le graphique n’est pas une droite l’on peut dire que la loi d’ohm n’est pas respectée pour les ampoules.
Cela s’explique par la variation continuelle de la température du filament qui a une incidence sur la résistance globale de l’ampoule.
Conclusion :
Une ampoule a un comportement qui n’est pas le même que les résistances, l’on peut dire que ce sont des résistances particulières.
Les résistances courantes sont constituées d’un matériaux qui n’est généralement pas affecté par la température.
Les ampoules subissent des variations de température qui influencent continuellement la résistance. Cela explique pourquoi ces dernières ne sont pas conformes à la règle générale : U=RI.
Graphiques :