Il est impératif, pour ne pas violer le postulat qui affirme que tous les référentiels inertiels sont équivalents, qu’une observation effectuée depuis un système inertiel dans un autre système en translation rectiligne uniforme par rapport au premier conduise aux mêmes résultats que l’observation effectuée depuis le second sur le premier.

Description

Deux événements simultanés et séparés par une distance de 1 m dans Σ sont observés depuis Σ’. Deux événements se produisant au même endroit et séparés par 1 m de temps dans Σ sont observés depuis Σ’.

Questions

1. Comment un observateur de Σ’ en translation rectiligne uniforme à la vitesse $\beta$ par rapport à Σ perçoit-il ce mètre d’espace et ce mètre de temps ?
2. Démontrez que les conclusions et les résultats sont les mêmes si on remplace Σ par Σ’ dans l’énoncé et dans la question 1.
3. Que vaut, pour l’observateur, la séparation en m entre ces deux paires d’événements ?

Réponses

Dessinons les diagrammes d’espace-temps des deux systèmes dont les origines coïncident au temps t=0 et plaçons les événements :

En projetant le mètre d’espace d’un système dans l’autre sans changer sa valeur dans le système de l’observé, on constate qu’il apparaît contracté aux deux observateurs.
En projetant le mètre de temps d’un système dans l’autre sans changer sa valeur dans le système de l’observateur, on constate qu’il apparaît dilaté aux deux observateurs.

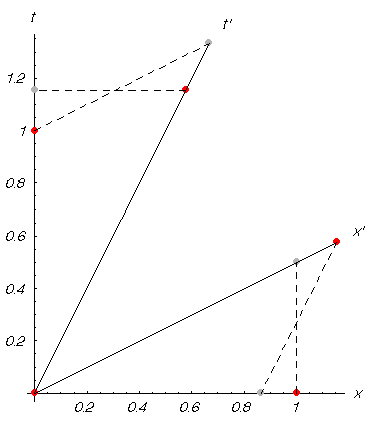
Le mètre d’espace d’un système observé depuis l’autre vaudra $\sqrt{1-\beta^2}$ m et le mètre de temps d’un système observé depuis l’autre $\frac{1}{\sqrt{1-\beta^2}}$ m.

Conclusions
– La détermination de la longueur maximale d’une règle est toujours celle que réalise un observateur du système propre.
– La détermination d’une durée minimale est toujours celle que réalise un observateur du système propre.