Détermination de la trajectoire d’une bille sur un plan incliné ainsi que de son accélération et de sa vitesse depuis deux hauteurs différentes.
par Mélanie Boninsegni, Nemo Rime, Vitangelo Pagliarulo
Tout d’abord, nous avons placé un calque, afin d’avoir une trace de la trajectoire de la bille. Nous avons ensuite lâché la bille six fois de deux hauteurs différentes, dont nous avons relevé les temps de parcours et fait une moyenne. Il faut prendre en compte le fait qu’au point de départ la direction de la vitesse initiale est horizontale.
Ensuite, nous avons détaché le calque et mesuré les coordonnées (x ;y) de 6 points sur chacune des trajectoires obtenues, en fixant l’origine du système d’axes au point de lancement.
Puis pour finir, nous avons calculé, à l’aide de l’ordinateur, l’équation de chaque trajectoire à partir des points relevés, et déduit de ces équations la vitesse initiale de la bille, sa vitesse finale et son accélération.
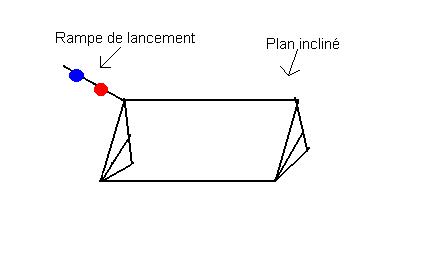
En rouge le premier point de départ, et en bleu le deuxième.
Voici les trajectoires obtenue sur le calque.
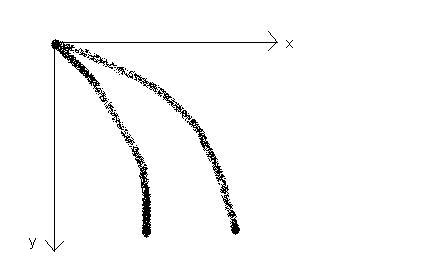
Valeurs trouvées lors de l’expérience
Après avoir obtenu la trace de la trajectoire de la bille, pour les deux différentes hauteurs, nous avons mesuré la distance sur l’axe x entre le point de départ et le point final de la trajectoire de celle ci dans chaque cas. Pour la première hauteur, la distance vaut 0.23 [m]. Pour la deuxième hauteur, la distance vaut 0.103 [m].
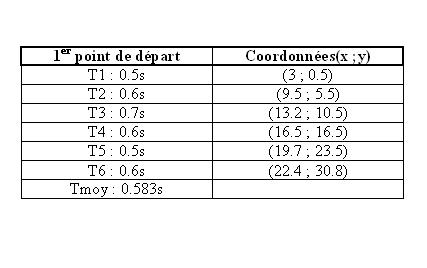
Nous avons trouvé les équations de "y", à l’aide de Mathematica, qui fournit les équations par ajustage d’une parabole sur les points de mesure.
Connaissant la distance parcourue par la bille sur l’axe x, ainsi que son temps de chute, nous pouvons en déduire, que la vitesse initiale vaut X/T.
Pour l’accélération : nous connaissons la formule y=1/2*a*t^2, ce qui revient à écrire que y=1/2*a*(x/v)^2. Après isolation de "a", nous obtenons : a=2*Vi^2*y.
Équation : y=0.060955x^2
Vitesse initiale=0.3945 [m/s]
Accélération=0.01897 [m/s^2]
Vitesse finale=0.406 [m/2]
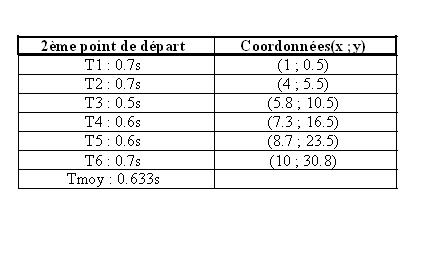
Équation : y=0.309645x^2
Vitesse initiale=0.0.1627 [m/s]
Accélération=0.01639 [m/s^2]
Vitesse finale=0.173 [m/2]
Questions :
1. Pour pouvoir déterminer jusqu’où va une bille lorsqu’on la lance il faut connaître sa position initiale, son accélération, sa vitesse initiale, l’inclinaison du plan et les éventuelles forces de frottement.
La question correcte serait donc : si on lance une bille depuis une position Xo à une vitesse Vi et dans une direction y. Quelle distance parcoure la bille jusqu’à ce que sa vitesse finale soit nulle ?
2. En admetant que la bille soit pleine et que nous nous trouvions sur terre, l’accéleration en l’absence de frottements dépend de l’inclinaison du plan, si cela se passait sur une autre planète, il faudrait tenir compte de la force pesante de cette planète.
3. Non, l’accéleration ne dépend que de l’inclinaison du plan et de l’attraction terrestre. La masse n’influe pas sur son accéleration.
4. Ces deux mouvements sont similaires, la bille est, dans les deux cas, soumise à une force constante en direction et en grandeur, la différence est que sur un plan incliné, les choses se passent plus lentement.
