La charge q sur une plaque d’un condensateur est proportionnelle à la différence de potentiel V entre les plaques du condensateur.
par Blaise Hakizimana, Gael Burkardt, Sam Fasih
OBJECTIFS
– Mesurer la constante de temps d’un circuit RC.
– Comparer celle-ci à la valeur prévue (R fois C).
– Mesurer la différence de potentiel entre les plaques d’un condensateur en fonction du temps, à la charge et à la décharge.
– Ajuster une fonction aux données. L’un des paramètres correspond à une constante de temps expérimentale.
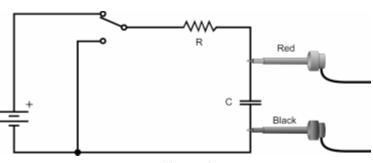
MATERIEL
- Ordinateur
- LabPro
- Logger Pro
- Sonde de tension Vernier
- Fils de connexion
- Condensateur non polarisé de 10-micro F
- Résistances de 100-kilo ohm, 47-kilo ohm
- Piles ou alimentation
- Commutateur
QUESTIONS PREALABLES
1) Soit une boule de verre contenant des bonbons, avec 1000 bonbons au départ. Vous passez à côté une fois par heure. Comme vous voulez que personne ne remarque que vous prenez des bonbons, vous prenez à chaque fois 10% des bonbons restant dans la boule. Faites un graphique du nombre de bonbons restants pour les quelques premières heures.
2) Si vous enleviez 20% des bonbons, comment le graphique changerait-il ? Esquissez le nouveau graphique.

rouge:graphique pour la question 1)
bleu : graphique pour la question 2)
PROCEDURE
– Comparez l’équation de l’ajustement au modèle proposé pour la décharge du condensateur dans l’introduction
$V(t) = V_{0}*e^{-t/RC}$
– Quel est le lien entre c de l’ajustement et la constante de temps du circuit définie dans l’introduction ?
1/c = RC. La constante de temps RC est égale à l’inverse du c de l’ajustement.
TABLEAU
| essai | paramètres | résistance en ohm | 1/c | constante de temps en s |
|---|---|---|---|---|
| charge | A=3.1 / B=-0.3 / C=1.1 | 0.9 | 100000 | 1 |
| décharge | A=3 / B=0 / C=1 | 0.9 | 100000 | 1 |
| charge | A=4.2 / B=-1.3 / C=2.3 | 0.4 | 47000 | 0.47 |
| décharge | A=4 / B=0 / C=2.3 | 0.4 | 47000 | 0.47 |
GRAPHIQUES

Charge avec R=100kΩ (potentiel [V] en fonction du temps [s])

Décharge avec R=100kΩ (potentiel [V] en fonction du temps [s])
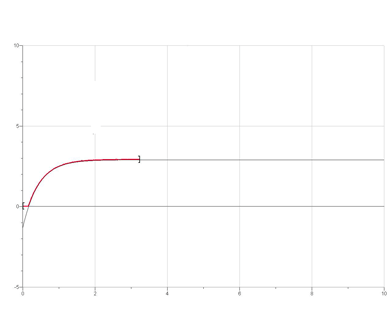
Charge avec R=47kΩ (potentiel [V] en fonction du temps [s])
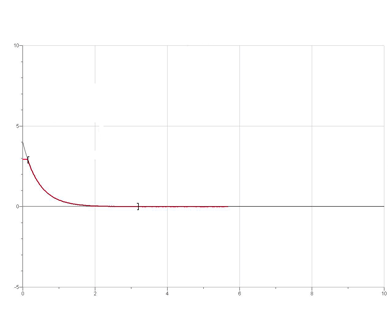
Décharge avec R=47kΩ (potentiel [V] en fonction du temps [s])
ANALYSE
– Notez que les résistances et les capacités ne sont pas données comme des valeurs exactes, mais seulement comme des valeurs approximatives avec une tolérance. S’il y a un désaccord entre les deux quantités comparées dans la question 2, les tolérances peuvent-elles expliquer la différence ?
Nous pouvons remarquer dans le tableau de mesure que RC n’est pas tout à fait égal à 1/c, mais cette différence est comblée par la tolérance.
– Quel est l’effet de la diminution de la résistance sur la décharge du condensateur ?
Le courant circulant plus facilement à travers le circuit lorsque nous diminuons la résistance, la décharge se produit plus vite.
– Quelle est la signification de la pente du graphique de ln (V) en fonction du temps pour la décharge ?
La pente de ln (V) correspond à l’inverse de la constante de temps RC.
EXTENSION
– Quel pourcentage de la tension initiale reste-il après une constante de temps ? Et deux ? Et trois ?
Pour la charge :
Pour calculer le pourcentage de la charge nous avons utilisé la formule de la charge. Nous avons ensuite remplacé t par 1, 2 ou 3 RC. ce qui nous donne les résultats suivants.
Pour la décharge :
La méthode est la même sauf que nous avons utilisé la formule pour la décharge.
| Constante de temps | Charge | Décharge | total |
|---|---|---|---|
| 1RC | 63,2 % | 36,8 % | 100% |
| 2RC | 87,5 % | 12,5 % | 100% |
| 3RC | 94 % | 6 % | 100% |