Rapport de la séance de laboratoire du 03.11.2006 sur les chutes verticales.
par Andreï Jourovski, Thierry Fuglister
La mesure du temps de parcours d’une bille pour différentes hauteurs de chute permet de déterminer son accélération. Pour une bille en acier et des hauteurs de l’ordre du mètre, on peut négliger la force de frottement due à l’air et l’accélération obtenue correspond à l’accélération terrestre.
Expérience :
1. On mesure le temps de chute d’une bille pour 6 hauteurs différentes avec 4 mesures pour chaque hauteur puis on calcule le temps moyens de chute.
Voici nos résultats :
| # | Hauteurs | temps1 | temps2 | temps3 | temps4 | temps moyen |
| 1 | 0.4m | 0.305s | 0.310s | 0.308s | 0.306s | 0.307s |
| 2 | 0.5m | 0.322s | 0.325s | 0.322s | 0.322s | 0.323s |
| 3 | 0.6m | 0.353s | 0.352s | 0.353s | 0.350s | 0.352s |
| 4 | 0.7m | 0.381s | 0.385s | 0.382s | 0.381s | 0.382s |
| 5 | 0.8m | 0.408s | 0.410s | 0.411s | 0.413s | 0.410s |
| 6 | 0.9m | 0.432s | 0.432s | 0.436s | 0.432s | 0.433s |
2. On reporte les hauteurs de chute en fonction du temps élevé au carré.
Nous obtenons le graphique ci-dessous,
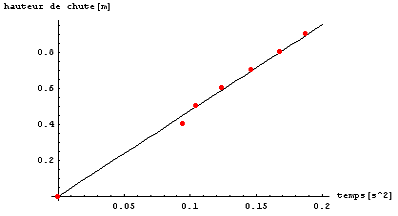
3. À partir de ce graphique nous pouvons déterminer l’accélération de ces mouvements,
$h=1/2at^2$
$ y=mx$
$1/2a=m$ -> $a=2m$
il nous suffit d’obtenir la pente (m=y/x) et de la doubler pour trouver l’accélération.
$a=\frac{2*1[m]}{0.2[s^2]}=10[m/s^2]$
4. Nous calculons la vitesse finale de la bille pour chaque hauteur de chute :
V finale=v0+at
| hauteurs | t moyen*a | vitesse finale |
| 0.4m | 0.307s * $10m/s^2$ | 3.07m/s |
| 0.5m | 0.323s * $10m/s^2$ | 3.23m/s |
| 0.6m | 0.352s * $10m/s^2$ | 3.52m/s |
| 0.7m | 0.382s * $10m/s^2$ | 3.82m/s |
| 0.8m | 0.410s * $10m/s^2$ | 4.1m/s |
| 0.9m | 0.433s * $10m/s^2$ | 4.33m/s |
5. On reporte les vitesses finales calculées en fonction de la hauteur puis en fonction du temps chute :
– vitesse en fonction de la hauteur de chute :

– vitesse en fonction du temps de chute :

N.B. Les unités utilisées en abscisse sont des dixièmes de s et pas des s.
Réponses au questions du protocole :
- Horaire de la bille : $r(t)=r0 + v0t + 1/2at^2$
- Formules permettant d’obtenir :
- la vitesse en fonction du temps et de l’accélération : $V=at$
- la vitesse en fonction du chemin parcouru (ici:hauteur) et de l’accélération :
$v=at -> t=v/a$
$h=1/2at^2$ on remplace le temps (t) par $v/a$—>$h=1/2a\frac{v^2}{a^2}$
$h=\frac{v^2}{2a}$ de là on obtient $v^2=2ah$ -> $v=\sqrt{2ah}$
- Quelques situations de chute avec le vecteurs accélération et de vitesse lorsque nous lançons une balle verticalement vers le haut :
-
- la balle s’élève ;

- la balle s’élève ;
-
- la balle a atteint le point le plus haut ;

- la balle a atteint le point le plus haut ;
-
- la balle redescend ;

- la balle redescend ;
Pour un parachutiste, la force de frottement due à l’air n’est pas négligeable. Sa vitesse finit par se stabiliser, même si le parachute reste fermé. Le graphique ci-dessous donne l’évolution de la vitesse d’un parachutiste (en m/s) en fonction du temps (en s). Estimez, à partir de ce graphique :
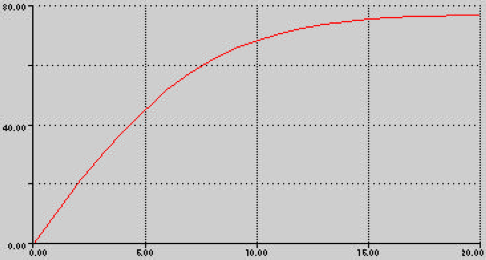
-l’accélération initiale du parachutiste correspond à la pente de la tangente au point initial :
$a(0)= \frac{50[m/s]}{5[s]}=10[m/s^2]$

– La distance parcourue par le parachutiste en 20 secondes correspond à l’aire du graphique en bleu ci-dessus, soit environ 1165m.
– On compare la distance obtenu par la distance que le parachutiste aurait atteint en 20 secondes sans frottement :
Avec frottement : 1165m
Sans frottement : $d=1/2at^2$
$d=1/2*10[m/s^2]*20^2[s^2]=2000m$
Cette grande différence est uniquement due à la force de frottement, qui stabilise la vitesse du parachutiste à environ 75[m/s], tandis que sans frottement le parachutiste va atteindre une vitesse de 200[m/s] après 20 secondes. ($v=at -> v=10[m/s^2]*20[s]=200[m/s]$)
En conclusion, ce travail nous a appris à faire des relations entre la hauteur, le temps de chute, l’accélération et de déterminer des formules pour des problèmes de l’ordre d’une chute verticale sans frottement (les hauteurs sont si petites que cette force est négligeable).
