Étude de la chute verticale d’une bille en fer dans de la glycérine.
Voici un article expliquant et illustrant la chute verticale d’une bille (en fer) dans un liquide visqueux (de la glycérine) ainsi qu’un graphique illustrant l’évolution de la position, la vitesse ainsi que l’accélération de cette bille au cours du temps.
Description
On lâche une bille en fer de 0.01 kg dont la masse volumique vaut 7.87 kg/dm3 dans un liquide visqueux (la glycérine) dont la masse volumique vaut 1.26 kg/dm3. La vitesse initiale de la bille est nulle tout comme sa position initiale. Le flux de la vitesse est égal à la vitesse. Durant sa chute verticale, elle est soumise à trois forces : son poids dirigé vers le bas, la force d’Archimède et une force de frottement due au liquide, dirigées vers le haut. Son accélération est égale, selon la loi fondamentale de la dynamique, à la somme des forces qu’elle subit divisée par sa masse.
Le mouvement d’une chute d’une bille dans un liquide visqueux ne s’effectue que sur le plan vertical, c’est-à-dire selon l’axe des ordonnées (y).
La gravitation (ou accélération) terrestre équivaut à 9,81 m/s2.
Tableau des différentes données numériques :
| SUJET | SYMBOLES | FORMULES | UNITÉS |
| Position | y | / | m |
| Vitesse | v | / | m/s |
| Accélération | a | (Poids - F archi - F frott )/m bille | m/s2 |
| Flux de la vitesse | Flux v | / | m/s |
| Masse de la bille | m bille | / | kg |
| Volume de la bille | vol | M bille / rho bille | dm3 |
| Masse volumique de la bille | rho bille | / | kg/dm3 |
| Masse volumique du liquide | rho liqu | / | kg/dm3 |
| Gravitation terrestre | g | / | m/s2 |
| Force de pesanteur | Poids | m bille *g | N |
| Force de frottement | F frott | 0.4* v | N |
| Force d’Archimède | F archi | rho liqu * g* vol bille | N |
Comment réaliser un modèle Stella illustrant la chute d’une bille dans un liquide visqueux ?
Tout d’abord réalisez le modèle de base de Stella ; c’est-à-dire prendre un réservoir et le relier à un flux. La liaison entre les deux doit être « biflow ». Ensuite copiez et collez ce premier modèle, ainsi vous obtiendrez le modèle de base de Stella constitué de deux réservoirs et de deux flux. Nommez-les « a », « v », « flux v » et « y ». Reliez d’une flèche « v » à « flux v » puis attribuez à chacun des quatre éléments leurs valeurs respectives mentionnées dans l’énoncé.

Ajoutez autant de petits cercles (éléments tiers) qu’il y a d’éléments à placer, puis nommez-les « m bille », « vol bille », « rho bille »,« rho liqu », « g », « Poids », « F frott », « F archi ».
Ensuite reliez par des flèches les différents éléments (moyen mnémotechnique : les flèches partent des différents composants du calcul et se dirigent vers l’élément défini par ce calcul. Par exemple, selon la formule inscrite dans le tableau ci-dessus, « Poids=m bille *g », donc les flèches partent de « m bille » et « g » et se dirigent vers le « Poids »).
Voici le modèle Stella illustrant les données ci-dessus :

Voici le graphique correspondant au modèle Stella ci-dessus :
C’est un aperçu de l’allure du graphique entre 0 et 5 secondes.
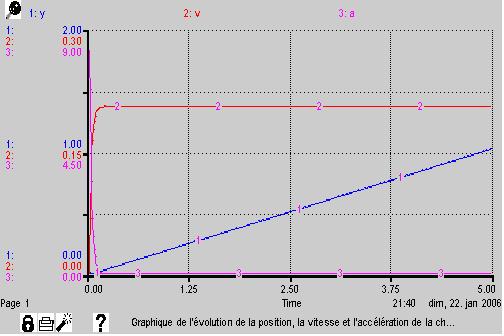
Comment réaliser le graphique illustrant l’évolution de la position, de la vitesse ainsi que de l’accélération de la bille ?
Cliquez sur le petit graphique rose puis cliquer quelque part sur votre feuille, ensuite cliquez deux fois sur le graphique, demandez un graphique « Time Series » afin de faire apparaître la position, la vitesse ainsi que l’accélération de la bille en fonction du temps. Cliquez deux fois sur « y », « v » et « a » pour les faire apparaître dans le tableau de droite. Cliquer sur ok puis sur « Run » et « Run », le graphique apparaîtra. Ensuite cliquez à nouveau sur « Run » et « Run specs… », à côté de « DT » mettez comme valeur 0,01 (pour affiner le pas) et en dessous de « Integration Method » sélectionnez « Runge-Kutta 4 » comme méthode de calcul (c’est la méthode de calcul la plus précise). Cliquez à nouveau sur « Run » et « Run », la version finale de votre graphique apparaîtra. (La position est exprimée en m, la vitesse en m/s, l’accélération en m/s2 et le temps en s).
Voici un autre graphique correspondant au modèle Stella ci-dessus :
C’est un aperçu de l’allure du graphique entre 0 et 0,05 secondes.

Comment faire varier les pas ainsi que les lapses de temps durant lesquelles sont prises les différentes mesures ?
Dans « Run » cliquez sur « Run specs… », puis dans « Length of simulation » à côté de « From » inscrivez « 0 », puis à côté de « To » inscrivez « 5 » et à côté de « DT » inscrivez 0,01. Cela signifie que les différents points de votre graphique se traceront jusqu’au temps limite de 5 secondes. C’est-à-dire que sur votre graphique vous lirez les différentes positions, vitesses et accélérations de la bille entre 0 et 5 secondes et par pas de 0,01 secondes. Vous pouvez bien sûr faire varier le lapse de temps selon que vous désiriez une vision plus précise ou au contraire une vue d’ensemble de l’évolution des différentes courbes du graphique.
Voici quelques questions auxquelles Stella nous permet de répondre :
– Quelle vitesse maximale, en m/s, la bille atteint-elle ?
- Réponse : 0,21 m/s
– Quelle distance, en m, doit-elle parcourir pour atteindre cette vitesse maximale ?
- Réponse : 0,02 m
– Au bout de combien de temps, en s, atteint-elle sa vitesse maximale ?
- Réponse : 0,14 s
– Quelle accélération minimale, en m/s2, la bille atteint-elle ?
- Réponse : 0 m/s2
– Au bout de combien de temps, en s, atteint-elle son accélération minimale ?
- Réponse : 0,2 s
Pour trouver ces différentes valeurs, faites glisser votre curseur sur votre graphique.
Conclusion
En conclusion, nous remarquons que Stella est un programme avec lequel on peut interagir avec des flux, des réservoirs, des facteurs tiers à l’aide de connecteurs, et nous permet de résoudre assez facilement des problèmes difficilement réalisables par écrit. De plus, Stella nous permet d’obtenir des représentations graphiques illustrant différentes situations.
