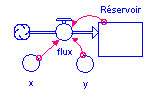
Stella est un intégrateur numérique. On travaille avec des réservoirs que l’on peut remplir ou vider à l’aide de flux.
Qu’est-ce que Stella ?
Stella est un intégrateur numérique. Voici une définition provenant du site owl-spip.ch :
"Lorsqu’on lance une simulation avec un modèle comportant un flux connecté à un réservoir, STELLA calcule à chaque pas une aire élémentaire et ajoute le résultat au contenu du réservoir. Cette aire est approximée par celle d’un petit rectangle dont la hauteur est donnée par la hauteur de la courbe en ce temps là et dont la base est égale au pas d’intégration dt. Le nombre de rectangles est déterminé par la durée de la simulation : $n= (tmax-tmin)/dt$". (http://owl-spip.ch/spip.php?article178, date de consultation : 16.12.2007)
On travaille donc avec des réservoirs que l’on peut remplir ou vider à l’aide de flux. On peut par ailleurs faire intervenir des facteurs tiers.
Obtention d’une croissance linéaire
La méthode la plus simple pour obtenir une croissance linéaire à l’aide de stella consiste à créer un modèle avec un réservoir et un flux. Lorsque le temps s’écoule le flux fait augmenter la valeur du réservoir de façon constante.
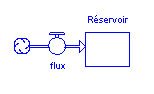
Dans un modèle de croissance linéaire le flux ne doit pas dépendre de la valeur du réservoir. On veut que le flux soit toujours constant. Si l’on crée un lien entre le réservoir et le flux (comme dans l’image ci-dessous), il faut que "réservoir" apparaisse dans la définition de ce dernier ; mais cela ne doit pas avoir d’influence sur le flux, sinon la croissance n’est plus linéaire (elle serait par exemple être exponentielle si l’on effectuait : $flux = réservoir$, où INITIAL(Réservoir) ? 0).
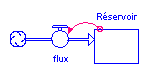
Pour neutraliser l’effet du réservoir sur le débit on effectue réservoir-réservoir. Le flux est défini de la façon suivante : $réservoir-réservoir+x$. Plus $x$ sera grand, plus vite augmentera la valeur du réservoir.
Lorsqu’on trace le graphique d’une croissance linéaire on obtient une droite affine.
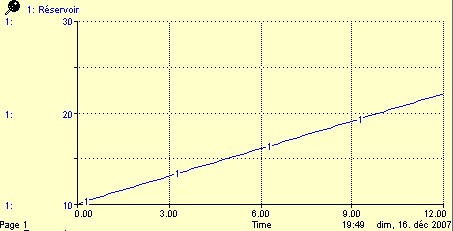
Une fonction affine est de forme $ax + b$. Dans notre modèle Stella, le coéfficient $a$ est le flux et $b$ la valeur initiale du réservoir. Plus on avance dans le temps - qui correspond à $x$ - plus $ax$ est grand, mais augmente de façon constante. Sur le graphique ci-dessous on peut voir en rouge la valeur $b$, qui correspond à ce qui se trouve dans le reservoir initialement et qui va y rester. En vert est représenté $ax$.
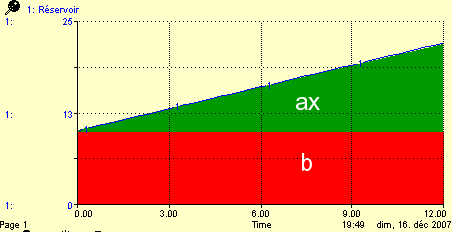
Comme $a$ correspond à la pente du graphique on peut l’insérer dans une variable séparée (en vue, par exemple d’etudier ce qui se passe lorsque celle-ci varie). On peut aussi définir deux variables $x$ et $y$ et flux = $réservoir-réservoir+\frac{y}{x}$. On peut ainsi définir la fonction à l’aide de coordonnées cartésiennes (en modifiant $x$ et $y$).