Lorsqu’un mobile se déplace dans un champ de force uniforme - comme le champ de la pesanteur au voisinage de la surface terrestre - et qu’il est soumis à son seul poids, son horaire, qui correspond aux équations paramétriques du mouvement, permet d’obtenir plusieurs informations sur sa trajectoire.

Horaire d’un tir parabolique :

Lorsqu’un mobile se déplace au voisinage de la surface terrestre et qu’on néglige le frottement, il est soumis à une force constante qui est son poids. Son horaire est alors celui d’un mouvement dont le vecteur accélération est constant. Cet horaire s’écrit :

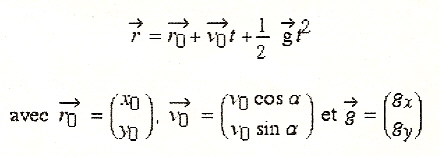
Horaire d’un mouvement dans un champ de force uniforme.
Le mouvement d’un projectile soumis à son seul poids est un mouvement uniformément accéléré (accélération constante).

En choisissant un système d’axes Oxy dont l’axe y est aligné sur le poids du mobile, on annule la composante gx de l’accélération et la composante gy est alors égale à -9.81 m/s^2 :

– gx=0

– gy=-9.81 m/s^2

Équations paramétriques et équation de la trajectoire :

En écrivant cet horaire en composantes, on obtient deux équations appelées équations paramétriques du mouvement (c’est le temps t qui est le paramètre). En éliminant t entre ces deux équations, on obtient l’équation de la trajectoire.

En résumé, les équations paramétriques nous permettent de trouver x et y en fonction du temps, c’est le temps qui est le paramètre.

Exercice :

Démontrez, en utilisant les équations paramétriques obtenues à partir de l’horaire ci-dessus, que la trajectoire est une parabole.
Exprimez, puis calculez, en utilisant les valeurs numériques suivantes x0=0, y0=0, v0=20 m/s,
gy=-9.81 m/s^2, tinitial=0, tfinal=3,5 s, Δt=0.5 s, α=60° :

– les composantes des vecteurs position, vitesse et
accélération.

L’horaire des vecteurs position nous est donné (selon l’horaire de départ) par :

– x(t)=x0+v0*cos(α)*t

– y(t)=y0+v0*sin(α)*t+(1/2)*(gy)*t^2

L’horaire des vecteurs vitesse est obtenu par la dérivée de l’horaire des vecteurs position :

– vx=v0*cos(α)

– vy=v0*sin(α)+2*(1/2)*(gy)*t

L’horaire des vecteurs accélération nous est donnée par la dérivée de l’horaire des vecteurs vitesse :

– ax=0

– ay=gy

En utilisant les valeurs numériques de l’énoncé dans les horaires ci-dessus, on aura une variation des coordonnées en fonction du temps (de 0 à 3 secondes avec un pas de 0.5 seconde), on obtiendra alors un tableau avec les valeurs suivantes (arrondies au centième près) :

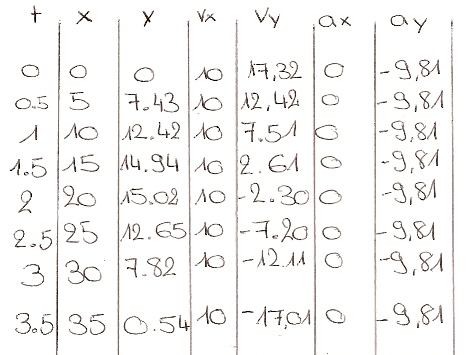
En utilisant les coordonnées ci-dessus, on peut obtenir les vecteurs des horaires position, vitesse et accélération, comme on peut le voir sur le graphique
ci-dessous.

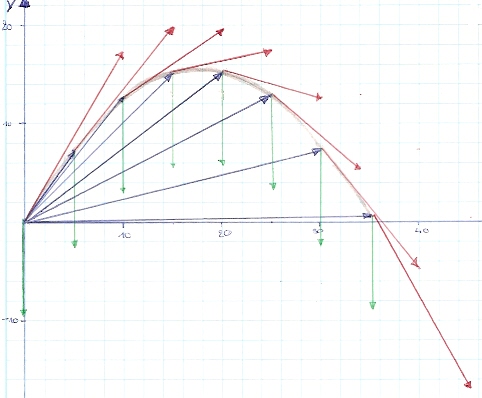
– Flèches bleue, vecteur position (x et y).
– Flèches rouge, vecteur vitesse (vx et vy).
– Flèches verte, vecteur accélération (ax et ay).
– En gris, la trajectoire nous décrit bien une parabole.

C’est grâce aux vecteurs position que l’on peut voir que notre trajectoire décrit bien une parabole.