Comportements, modèles et équations différentielles
Épreuve d’applications des mathématiques
Exercices sur la modélisation de comportements, sur les équations différentielles associées et sur la recherche des solutions.
Logistic Equation from the Wolfram Demonstrations Project by Jeff Bryant
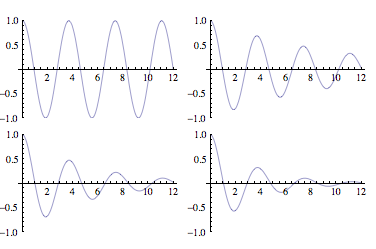
- Construisez le modèle Stella permettant d’obtenir les comportements ci-dessous.
- Donnez la valeur des paramètres pour chaque graphique.
- Écrivez l’équation différentielle associée à votre modèle.
- Résolvez cette équation avec Mathematica et donnez sa solution générale.
- Donnez un exemple de phénomène qui pourrait être décrit par ce modèle.
- Donnez la signification des paramètres dans cet exemple.
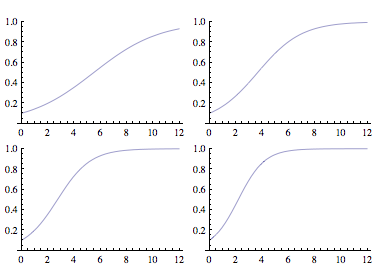
Comportements
- Construisez le modèle Stella permettant d’obtenir les comportements ci-dessous.
- Donnez la valeur des paramètres pour chaque graphique.
- Écrivez l’équation différentielle associée à votre modèle.
- Résolvez cette équation avec Mathematica et donnez sa solution générale.
- Donnez un exemple de phénomène qui pourrait être décrit par ce modèle.
- Donnez la signification des paramètres dans cet exemple.
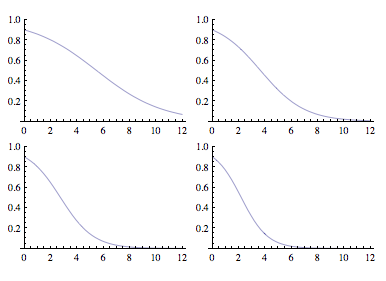
- Construisez le modèle Stella permettant d’obtenir les comportements ci-dessous.
- Donnez la valeur des paramètres pour chaque graphique.
- Écrivez l’équation différentielle associée à votre modèle.
- Résolvez cette équation avec Mathematica et donnez sa solution générale.
- Si la courbe représente la charge d’un condensateur au travers d’une résistance, que vaut la constante du temps τ du circuit dans chaque cas ?
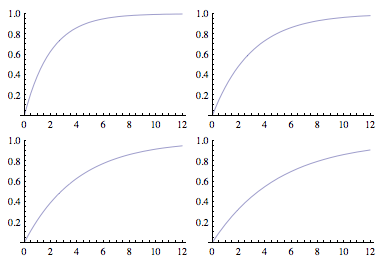
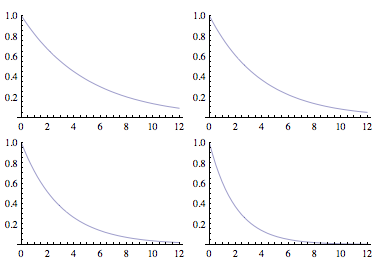
- Construisez le modèle Stella permettant d’obtenir les comportements ci-dessous.
- Donnez la valeur des paramètres pour chaque graphique.
- Écrivez l’équation différentielle associée à votre modèle.
- Résolvez cette équation avec Mathematica et donnez sa solution générale.
- Si la courbe représente le déclin d’une population, que vaut la demi-vie des individus dans chaque cas ?
Une masse de 500 g est accrochée à un ressort et oscille.
- Que vaut la raideur k du ressort si les unités des axes sont celles du SI ?
- Construisez le modèle Stella permettant de simuler les oscillations.
- Écrivez l’équation différentielle associée à votre modèle.
- Résolvez cette équation avec Mathematica et donnez sa solution générale lorsqu’il n’y a pas de frottement.
- Que vaut le coefficient de frottement (prop. à v) dans chaque cas ?