Étude des forces fictives d’inertie et centrifuge apparaissant dans un référentiel non-galiléen lorsqu’il est animé de mouvements simples par rapport aux référentiels d’inertie (d’après J.-A. Monard, Mécanique, Bienne 1977)
Dans certaines situations, il est commode de considérer un référentiel attaché à un corps accéléré - la Terre par exemple - par rapport aux référentiels d’inertie. Les lois de la mécanique doivent alors être modifiées pour rendre compte des mouvements observés dans un référentiel non-galiléen. Ces modifications consistent à introduire, en plus des forces réelles apparaissant dans un système d’inertie, des forces fictives appelées force d’inertie, force centrifuge et force de Coriolis. Ces forces d’inertie dépendent des mouvements du référentiel considéré par rapport aux référentiels d’inertie, notamment de l’accélération de son origine et de la rotation de ses axes.
Référentiel en translation uniformément accéléré
Considérons un véhicule en translation uniformément accélérée par rapport à un référentiel d’inertie Oxyz et attachons-lui un référentiel O’x’y’z’. Relativement au premier référentiel, les axes du second ont des directions fixes et son origine a un mouvement uniformément accéléré. Les vecteurs position r et r’ d’un point matériel quelconque M sont liés par la relation :
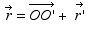
En dérivant deux fois de suite, on fait apparaître les vitesses et les accélérations du mobile, relativement aux deux référentiels :
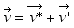
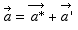
L’observateur d’inertie écrit l’équation de Newton :
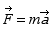
et compte tenu de ce qui précède, on peut écrire cette équation :
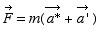
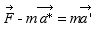
L’observateur dans le véhicule interprète le deuxième terme du membre de gauche comme une force d’inertie Fin et il écrit l’équation de Newton :
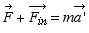
Ainsi, dans un référentiel en translation par rapport aux référentiels galiléens et ayant une accélération de grandeur a* relativement à eux, il faut introduire, sur tout objet de masse m, une force fictive d’inertie :
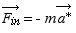
Référentiel en rotation uniforme
Supposons qu’un système tourne autour d’un des axes d’un référentiel galiléen Oxyz, autour de Oz par exemple, à une vitesse angulaire constante ω. Lions au système tournant un référentiel O’x’y’z’. Nous allons examiner les forces qui s’exercent sur un objet M, immobile par rapport au système tournant. Désignons par R la distance de l’objet à l’axe de rotation, et par m sa masse. Pour un observateur dans le système galiléen Oxyz, M a un mouvement circulaire uniforme. Sa vitesse vaut :
$v=\omega R$
Son accélération est dirigée vers le centre du cercle qu’il décrit et a pour grandeur :
$a=\omega^2 R$
D’après l’équation de Newton, la force qui s’exerce sur l’objet (ou la résultante des forces) est aussi dirigée vers ce centre. C’est la force centripète. Il s’agit d’une force réelle. Si l’objet est placé sur un plateau tournant, cette force est la force de frottement exercée par le plateau. Si l’objet est attaché à un fil, cette force est la force exercée par le fil, etc.
Pour un observateur lié au système tournant et travaillant avec ce système non-galiléen O’x’y’z’, l’objet M est immobile. Son accélération est nulle, et la somme des forces qui s’exercent sur lui est nulle. Pour cet observateur, une force d’inertie doit exister pour compenser la force réelle. Il écrira :
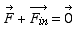
Cette force d’inertie fictive, qui est l’opposée de la force centripète, est appelée force centrifuge. Elle est perpendiculaire à l’axe de rotation et est orientée de façon à le fuir, d’où son nom. Sa grandeur vaut Fc = mω2R
Cette force n’est pas la même en tout point du référentiel comme dans le cas du référentiel en translation uniformément accéléré. Elle dépend de la distance de l’objet à l’axe de rotation.
Objet en mouvement dans un référentiel en rotation
Le cas ci-dessus ne constitue pas une étude complète du mouvement d’un point matériel dans un référentiel en rotation car nous nous sommes limités au cas de la statique dans un tel référentiel. Si on étudie des objets en mouvement par rapport à ce référentiel, il faut introduire une force d’inertie fictive supplémentaire appelée force de Coriolis. Cette force est proportionnelle à la vitesse v du mobile par rapport au référentiel en rotation et est donnée par :
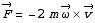
Voir les exercices sur les forces d’inertie
Pour en savoir plus
– Voir les effets de la force de Coriolis
– Expérience sur la force de Coriolis
– Modélisation de l’effet Coriolis
