Ce travail contient une brève explication de la découverte de l’effet papillon ainsi que des modèles Mathematica permettant de l’illustrer.
Le simple battement d’ailes d’un papillon pourrait déclencher un ouragan, voilà comment l’on décrit de façon simplifiée l’effet papillon. Cependant, cet effet semble bien plus compliqué à résumer qu’avec cette simple phrase. Mais au fond, qu’est-ce que l’effet papillon ? D’où vient-il ? Et comment peut-on le "représenter" avec Mathematica ?
En réalité l’effet papillon est une vulgarisation de la sensibilité aux conditions initiales, en effet, modifier infiniment une condition initiale peut entraîner sur le long terme des résultats totalement différents.
Historique
L’effet papillon tire son nom de la question qu’avait posé un jour Edward Lorenz, célèbre météorologue à une conférence : « Prédictibilité : le battement d’ailes d’un papillon au Brésil peut-il provoquer une tornade au Texas ? ».
Lorenz travaillait depuis longtemps avec un logiciel qui permettait de simuler l’évolution du temps à partir d’équations de bases qui tenaient compte des différents conditions atmosphériques, telles que le vent, la température etc. Les ordinateurs étant encore lents, il les laissaient tourner plusieurs jours durant, pour examiner comment évoluaient les paramètres de sa météo. Un jour, décidant d’examiner une séquence sur une plus grande période, il utilisa des données fournies par son imprimante à mi-parcours d’une séquence, pour ainsi gagner du temps. Il était persuadé que sa séquence reprendrait le fil de l’ancienne, puisque les chiffres étaient les mêmes. Pourtant, bien rapidement les courbes qui décrivaient sa météo "numérique" divergeaient par rapport aux anciennes qui avaient déjà été calculées.
Lorenz pensa d’abord qu’il s’était trompé en introduisant les chiffres, alors il examina ses données et comprit que la cause était autre. Pour effectuer ses calculs, l’ordinateur travaillait avec des nombres à six décimales. Mais afin d’économiser de la place, l’imprimante n’indiquait que les trois premières décimales. Lorsqu’il avait réintroduit les données, Lorenz avait utilisé les chiffres figurant sur la liste imprimée en supposant que la variation avec les paramètres complets mémorisés par l’ordinateur s’avérerait négligeable, puisqu’elle était de l’ordre de un pour mille. Pourtant, ces infimes différences d’un millième de degré pour la température ou d’un millième de mètre par seconde pour la vitesse du vent aboutissaient à des situations météorologiques complètement différentes lorsque l’ordinateur calculait l’évolution du climat sur une longue période. C’est de cette découverte qu’Edward Lorenz, "découvrit" l’effet papillon.
Illustrations
Voici quelques illustrations de la sensibilité aux conditions initiales, qui est en fait l’effet papillon.
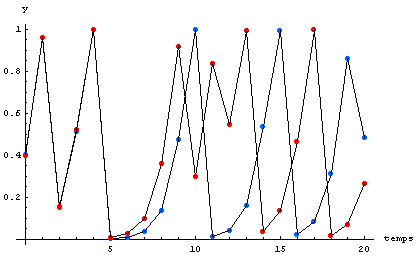
On voit ainsi très bien qu’en itérant la fonction $r*x(1-x)$ (qui permet d’obtenir le chaos), avec des valeurs initiales ayant seulement 1 millième de différence, le comportement change de manière radicale.
Pour obtenir ce graphique, voici le code utilisé :
Le f[x_] est la fonction de départ à itérer. Le x0 est la valeur initiale de départ et le t le temps sur lequel on souhaite itérer notre fonction.
Questions
Mais alors pourquoi parle-t-on "d’effet papillon" ?
En choisissant de parler de papillon et d’ouragan, Edward Lorenz voulait sans doute montrer que quelque chose de très minime, tels les battements d’ailes d’un papillon, pouvaient créer quelque chose d’énorme, un ouragan. Les termes "papillon" et "tornade" viennent sans aucun doute de son métier de météorologue. Cependant, il faut savoir que si les battements d’ailes d’un papillon peuvent créer une tornade, ils peuvent aussi éviter une tornade. Chaque battement ayant des répercussions différentes.
Les répercussions sont-elle dès lors infinies ?
En quelque sorte oui. Les répercussions peuvent être diverses et multiples. Comme on le voit sur ce graphique, en faisant varier la valeur de départ entre 0.1 et 0.4 par pas de 0.01, les différentes fonctions prennent pratiquement tout le graphique.
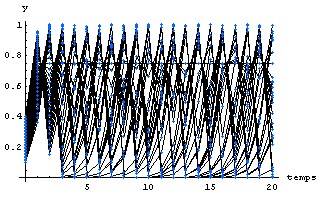
Pour obtenir ce graphique, voici le code utilisé :
Mais le véritable "effet papillon", est bien moins limité que ces illustrations ?
Oui bien sûr, les découvertes faites par Edward Lorenz sont basées sur des fonctions bien plus complexes. En réalité les graphiques créés ci-dessus ne sont qu’une illustration de la sensibilité aux conditions initiales, et non pas de l’effet papillon a proprement parler. Les variables utilisées par Lorenz étaient bien plus nombreuses et diverses, et faisaient intervenir beaucoup de facteurs.
Conclusion
Voilà ce qu’est, en conclusion, l’effet papillon. Il est bien sûr très difficile de l’illustrer, mes graphiques en sont d’ailleurs pas une explication. Ils ont juste comme but de montrer qu’une minime transformation peut complètement changer les données suivantes, ce qui est en fait la manière avec laquelle Edward Lorenz a découvert l’effet papillon. De ces modifications, il en a déduit qu’une chose microscopique, tels les battements d’ailes d’un papillon, pouvait radicalement modifier la météorologie. Les équations qu’il utilisait étaient sans doute bien plus compliquées que celle utilisé par mes soins.
Sources
– Extrait du texte "Le pouvoir du miroir" de Daniel Cordonier.
– Wikipedia
– owl-spip.ch
– Anciens notebook Mathematica, ainsi que le cours du premier semestre.
