Mesure du quotient e/m de l’électron en observant la trajectoire d’un faisceau d’électrons dans un champ magnétique.
Lorsqu’une particule chargée pénètre dans une région de l’espace où règne un champ magnétique homogène (entre deux bobines plates par exemple) elle subit une force perpendiculaire à son vecteur vitesse et aux lignes de champ. La particule décrit alors une trajectoire circulaire dont le rayon dépend du champ magnétique, de la masse, de la charge et de la vitesse de la particule. Connaissant la tension qui a permis d’accélérer la particule et le courant qui circule dans les bobines, on peut trouver respectivement la vitesse de la particule et le champ magnétique dans lequel elle évolue. La mesure du rayon de sa trajectoire permet alors de déterminer le rapport e/m de sa charge à sa masse.
Expérience
Nous utilisons un canon à électrons et nous observons le faisceau d’électrons de forme circulaire dans le champ magnétique uniforme formé par deux bobines de Helmholtz (on ne voit pas ces derniers, mais seulement l’impact des chocs contre des molécules d’hydrogène).
Nous avons donc mesuré le rayon (r) en mètres, du cercle formé par le faisceau en faisant varier le courant (I) de 0,8 à 2,2 [A] +/-10% et la tension (U) de 150 à 250 [V]+/-10%. Voir les mesures dans le tableau ci-dessous :
| 0.8[A] | 1[A] | 1.2[A] | 1.4[A] | 1.6[A] | 1.8[A] | 2[A] | 2.2[A] | |
|---|---|---|---|---|---|---|---|---|
| 150[V] | / | 0.091 | 0.077 | 0.063 | 0.054 | 0.05 | 0.045 | 0.04 |
| 200[V] | / | 0.113 | 0.09 | 0.078 | 0.066 | 0.056 | 0.05 | 0.046 |
| 250[V] | / | 0.12 | 0.105 | 0.09 | 0.075 | 0.065 | 0.057 | 0.05 |
Nous avons ensuite, représenté les rayons mesurés selon l’inverse de l’intensité :
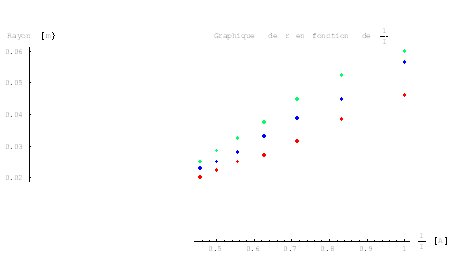
Légende du graphique ci-dessus :
– Points de couleur rouge : mesures avec une tension U de 150 [V]
– Points de couleur bleu : mesures avec une tension U de 200 [V]
– Points de couleur vert : mesures avec une tension U de 250 [V]
A l’aide de Mathematica on cherche la pente de chacune des trois fonctions, ce qui nous donne la valeur des trois coefficients k :
| 150[V] | 200[V] | 250[V] | |
|---|---|---|---|
| Pentes (x) | 0.045 | 0.054 | 0.06 |
On retrouve le coefficient k dans cette formule :
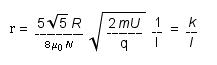
Nous résolvons ensuite cette équation pour isoler et déterminer m/q, en utilisant la valeur de 70 pour N (nombre de spires), 0,15 [m] pour R (le rayon des bobines) et en utilisant nos mesures.
| 150[V] | 200[V] | 250[V] | |
|---|---|---|---|
| m/q(x) | 1.32058 * 10-11 | 9.90435 * 10-12 | 7.92348 * 10-12 |
Une fois avoir determiné m/q nous pouvons calculer la valeur de m pour les trois cas (150, 200 et 250 [V]) sachant que q = 1,6 * 10-19 [C] :
| 150[V] | 200[V] | 250[V] | |
|---|---|---|---|
| m(x) | 2.11293 * 10-30 | 1.5847 * 10-30 | 1.26776 * 10-30 |
La valeur qui est indiquée dans la table CRM pour la masse d’un électron au repos est de : 9,10939 * 10-31 [kg]. On remarque une certaine différence entre les valeurs que nous avons trouvé et celle présente dans la table et l’erreur relative moyenne, calculée est de 80%. Cette différence est sûrement due à des erreurs de mesures au moment de la mesure du diamètre.
