par Alexandre Cacheiro, Rodrigo de Pablo Pena, Romuald Hausser
Cette experience a pour but de trouver expérimentalement le moment d’intertir de deux cylindres.
Introduction :
Nous allons étudier le moment d’inertie de deux cylindres roulant sur un plan incliné.
But :
Déterminer expérimentalement le moment d’inertie de deux cylindres.
Marche à suivre :
Nous avons pris différentes mesures sur la dimension des cylindres et leurs poids. Ensuite, nous les avons laissés rouler sur un plan incliné et avons collecté des mesures grâce à des cellules photoélectriques.
Matériel :
– Cylindre en Laiton de 1[kg] évidé
– Cylindre en Aluminium de 1[kg] plein
– Balance
– Pied à coulisse
– Règle
– Deux cellules photoélectriques
– Plan incliné
Mesures :

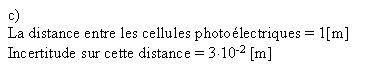

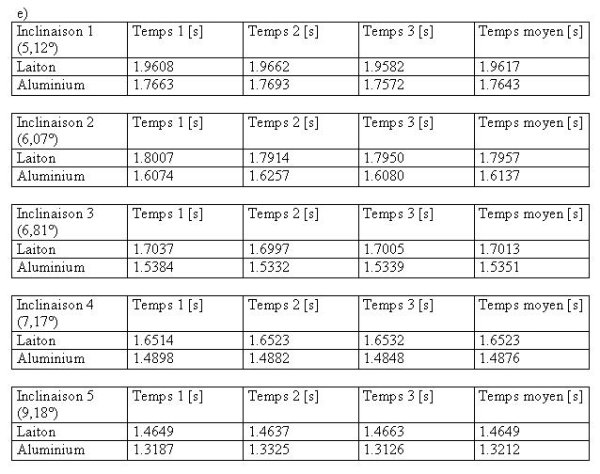
Calculs et graphiques :


e) En abscisse le sinus de l’angle et en ordonnée l’accélération en [ m/s²]
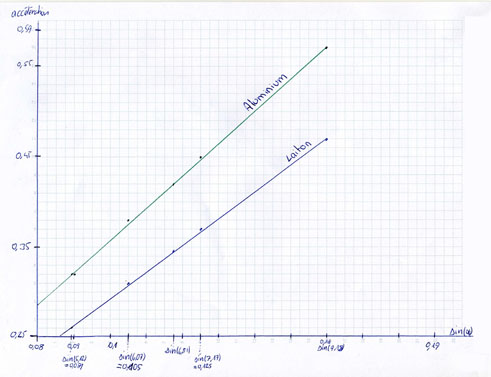
f)
Pentes :
– Laiton : 88/3
– Aluminium : 286/9
Comme le moment d’inertie est compris dans la pente des droites, nous pouvons en tirer la formule suivante :
I = ((m*r²*sin(teta)*g)-(m*r²*a))/a
Avec cette formule, nous trouvons les moments d’inertie suivants exprimés en [kg*m^2] :

Moyenne des moments d’inertie de l’Aluminium : 0.0010714 [kg*m^2]
Moyenne des moments d’inertie du Laiton : 0.0014671 [kg*m^2]
g)
Moments d’inertie trouvés à l’aide des formules de la Table.
– Aluminium : I = [m * r²] / 2 = 0.0003125 [kg*m^2]
– Laiton : I = Itot-Iint = 0.0006148 [kg*m^2]
En faisant les calculs, nous nous rendons compte que nos résultats sont pas mal différents de ceux trouvés à l’aide des formules de la Table. Comme dans cette expérience les mesures n’étaient pas d’une précision extrême, surtout lors de la mesure de l’angle d’inclinaison, nous pensons que c’est cela qui nous a amené à une telle différence dans nos résultats.
Conclusion :
Ce travail nous a pris beaucoup de temps, il y avait en effet un grand nombre de calculs à effectuer et la mise en page a aussi été très longue. Nous avons été déçus à la fin quand nos résultats n’ont pas bien coïncidé avec ceux calculés avec les formules données par la Table.