Temps de nage pour deux directions, l’une identique à celle du courant, l’autre perpendiculaire à celle du courant.
par bernard.vuilleumier
Nageurs dans un fleuve
Un nageur nage dans un fleuve à la vitesse c par rapport à l’eau. Il va d’un point A à un point B situés à terre et distants de L/2. L’eau se déplace de B vers A à la vitesse v.
Le même nageur nage maintenant sur le trajet ACA. La distance entre A et C est identique à la distance entre A et B mais la droite AC est perpendiculaire à la droite AB.
– Exprimez le temps de parcours du nageur pour chacun de ces trajets.
Deux nageurs quittent en même temps le point A à la même vitesse c par rapport à l’eau. Le premier va de A vers B puis revient en A en nageant d’abord contre le courant, puis avec le courant (la vitesse de ce dernier est v). L’autre va de A à C puis revient en A en nageant toujours avec le courant de côté.
– Quel est celui qui arrivera le premier en A ?
– Exprimez le décalage entre son arrivée et celle du second ?
Application numérique
– distance L=2km
– vitesse des nageurs par rapport à l’eau : c = 1.5 m/s
– vitesse du fleuve : v = 0.5 m/s
Corrigé
Lorsque un nageur remonte le courant, sa vitesse par rapport à la terre s’obtient en soustrayant la vitesse du fleuve à sa vitesse par rapport à l’eau, et lorsqu’il descend le courant, en additionnant ces deux vitesses. Le temps de « montée » s’obtient en divisant la distance qu’il franchit par sa vitesse « à la montée », et le temps de descente en divisant cette distance par sa vitesse « à la descente » :
La vitesse du nageur effectuant le trajet ACA est la somme vectorielle de sa vitesse par rapport à l’eau et de la vitesse du fleuve :
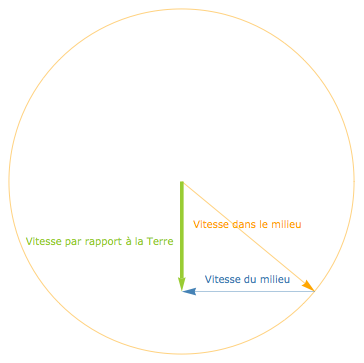
Le nageur qui arrive en premier est celui qui effectue le trajet ACA perpendiculaire à la vitesse du fleuve, car la racine de $1 -\frac{v^2}{c^2}$, quantité comprise entre 0 et 1, est plus grande que $1 -\frac{v^2}{c^2}$.
Le décalage temporel est donné par :
N. B. L’expression $\Delta t=\frac{L}{2c}\frac{v^2}{c^2}$, qui est obtenue par un développement en série au voisinage de 0, ne peut être utilisée que si v<<c.
Résultats numériques
– tABA = 1500 s
– tACA = 1414 s
– Δt = 86 s
– La formule approchée donne 74 s. [1]

