Cet article est une expérience qui a pour but de calculer la raideur k d’un ressort lors d’une expérimentation pratique.
par Aymeric Genet, Caroline Calpini
Ceci est un rapport de laboratoire de physique qui consiste à calculer la raideur k d’un ressort lorsque la période T de ce dernier est connue, et ainsi comparer les résultats obtenus lors de l’expérience pratique aux résultats théoriques.
I. But
Le but de notre laboratoire est de lier les différentes variables qui agissent lorsqu’un ressort oscille.
II. Oscillateur harmonique
Mesures
Ressort n°1
| Masse m (g) | 40g | 60g | 80g |
| Position x (m) | 0.886 | 0.781 | 0.713 |
| Période T (s) | 0.714 | 0.846 | 0.969 |
Ressort n°2
| Masse m (g) | 40g | 60g | 80g |
| Position x (m) | 0.761 | 0.706 | 0.655 |
| Période T (s) | 0.714 | 0.846 | 0.969 |
Nous n’avons pas calculé à la main les valeurs ci-dessus. Nous avons utilisé un programme informatique LabPro pour les calculer. Ces mesures sont donc calculées en minimisant les erreurs humaines.
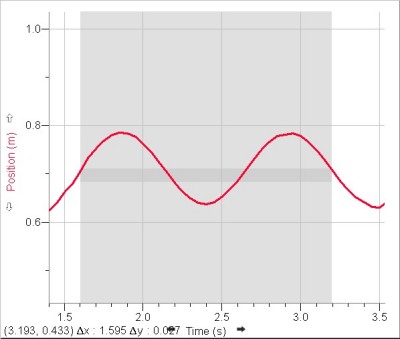
Questions
N.B. : Les mesures des questions 1. et 3. rejoignent la partie "Mesures" (tableaux plus haut).
2. Déterminez la constante k de chaque ressort à partir de ces mesures.
Prenons la loi de la dynamique $\vec{F} = -k \vec{x}$. À partir de cette équation, isolons la constante de la raideur k du ressort, ce qui nous donne :
$k = F/x$
Notez que le signe moins n’intervient pas dans ce calcul, car il détermine seulement la position de l’horaire sur la sinusoïde.
Pour le premier ressort, nous trouvons une raideur k = 14.28 ± 2.32 N/m
Pour le deuxième ressort, nous trouvons une raideur k = 4.58 ± 0.8 N/m.
4. Calculez à partir de vos mesures les constantes k et comparez avec les valeurs précédentes. S’il y a une différence, d’où peut-elle venir ?
Prenons la loi de la dynamique $T = 2 \pi \sqrt{\frac{m}{k}}$. À partir de cette équation, isolons la constante de la raideur k du ressort, ce qui nous donne :
$k =\frac{4 \pi^2 m}{T^2}$
Ainsi, pour le premier ressort, nous trouvons une raideur k = 15.35 ± 1.07 N/m.
Pour le deuxième, nous trouvons une raideur k = 3.75 ± 0.83 N/m.
5. Calculez la masse qui permet de doubler cette période T et vérifiez votre pronostic par l’expérience.
Reprenons l’équation de la période de l’oscillation $T = 2 \pi \sqrt{\frac{m}{k}}$. Remplaçons la valeur petit m par une inconnue de valeur grand M. Comme il est demandé de doubler cette période, multiplions le tout par 2, et substituons la valeur grand M.
$2T = 2 \pi \sqrt{\frac{M}{k}}$
$4T^2 = 4 \pi^2 \frac{M}{k}$
$\frac{4T^2 k}{4 \pi^2} = M$
Une fois substitué, remplaçons le T par son équation générale.
$M = \frac{16 \pi^2 \frac{m}{k} k}{4 \pi^2}$
La valeur k et $\pi^2$ se simplifient, il nous reste plus que :
$M = 4 m$
Ainsi, il nous faut une valeur de m quatre fois plus grande pour obtenir une période T deux fois plus grande.
Lors de notre expérience avec une masse de 10 g, nous avons obtenu une période T de 0.324 s. Si nous comparons avec la période d’une masse de 40 g, nous remarquons que les résultats sont presque doublés, de ± 0.033 s.
III. Pendule
Mesures
Angle : 30° ± 1°
| Longueur l (cm) | 52.9 | 47.2 | 41.9 |
| Période T (s) | 1.4534 | 1.3693 | 1.2937 |
| $g$ (m/s²) | 9.852 | 9.801 | 9.855 |
Questions
1. Calculez g à partir de la mesure de T pour différentes longueurs l.
Prenons l’équation de la période pour un pendule $T = 2 \pi \sqrt{\frac{l}{g}}$. À partir de cette équation, isolons l’attraction terrestre g, ce qui nous donne :
$g = (\frac{T}{2 \pi})^2 \frac{1}{l}$
Ainsi, si nous remplaçons les valeurs par nos mesures, nous trouvons une accélération terrestre de 9.828 ± 0.027 m/s².
2. Vérifiez que, pour de petites amplitudes d’oscillation, T est proportionnel à $\sqrt\frac{l}{g}$
Lors de notre expérience, nous avons mesuré des périodes T pour différentes longueur l, et nous avons remarqué que les périodes changeaient suivant la longueur l (voir tableau plus haut, dans la partie mesures).
Nous en concluons que la période dépend bien de la longueur l du pendule. Nous supposons également que la période T dépend de l’attraction terrestre g, mais nous n’avons pas encore expérimenté sur une autre planète.
3. Mesurez et reportez T en fonction de l’amplitude d’oscillation.
Dans l’équation de la période T d’un pendule, l’amplitude A de l’oscillation n’est pas tenue en compte, car elle n’est valable que pour des petites oscillations.
Durant notre expérience, nous avons pu remarquer que plus nous augmentions l’angle pour faire osciller le pendule, et plus la période T devenait grande.
Voici un tableau relatant nos mesures avec un différent angle :
| Angle $\alpha$ (°) | Période T (s) |
|---|---|
| 20 | 1.372 |
| 40 | 1.455 |
| 60 | 1.517 |
| 80 | 1.599 |
IV. Questions
1. Vérifiez que l’équation différentielle de l’oscillateur harmonique admet comme solution la fonction x(t)=Asin($\omega t+\phi$)
Tout d’abord, prenons la formule fondamentale de la dynamique : $\vec{F} = m\vec{a}$.
Substituons ce $\vec{F}$ dans la formule de la force de rappel d’un ressort $\vec{F} = -kx$ ce qui nous donne
$m\vec{a} = -kx$
L’accélération est la dérivée double de l’horaire. En la remplaçant, nous obtenons donc :
$m\ddot{x}(t) = -k x(t)$
La double dérivée de x(t) ($\ddot{x}(t)$) équivaut à la formule $\omega^2 A sin(\omega t+ \phi)$.
Nous savons également que la vitesse angulaire $\omega = \sqrt{\frac{k}{m}}$. Donc $\omega^2 = \frac{k}{m}$. Ainsi nous obtenons :
$m\frac{k}{m} A sin(\omega t + \phi) = -k x(t)$
En simplifiant, nous obtenons bien l’équation différentielle de l’oscillateur harmonique !
$Asin(\omega t+\phi) = x(t)$
2. Donnez une interprétation physique des grandeurs A, $\omega$ et$\phi$.
L’amplitude A détermine la distance entre le sommet de la sinusoïde et la position d’équilibre du mobile. Plus l’amplitude A est grande, plus la sinusoïde a de grandes courbes.
$\omega$ est la vitesse angulaire du mobile d’un MCU de rayon de l’amplitude A et de période T.
$\phi$ est la position de départ du mobile. C’est l’angle de départ, en radians, du cercle de rayon A.
3. Établissez, à partir des équations du mouvement de l’oscillateur harmonique et du pendule, l’expression donnant la période T d’oscillation.
Repartons de l’équation fondamentale de la dynamique $\vec{F} = m\vec{a}$ et la force de rappel d’un ressort $\vec{F} = -kx$, c’est-à-dire :
$m\vec{a} = -kx$
D’ici, substituons l’accélération par la dérivée double de x(t), soit :
$m\ddot{x}(t) = -k x(t)$
Mais cette fois-ci, remplaçons les deux horaires du pendule $\ddot{x}(t)$ ainsi que $x(t)$ par leurs équations. Nous obtenons ainsi cette formule :
$m \omega^2 A sin(\omega t+ \phi) = - k A sin(\omega t+ \phi)$
Si nous simplifions cette formule, nous obtenons $\omega^2 = \frac{m}{k}$.
Et en partant de l’équation $\omega T = 2 \pi$, nous obtenons bien que :
$T = 2 \pi \sqrt{\frac{m}{k}$
V. Conclusion
Grâce à cette expérimentation, nous avons pu obtenir une vision plus approfondie du mouvement harmonique simple et de l’oscillation d’un pendule, et ainsi, nous avons désormais des idées plus claires de ce que ces valeurs influencent sur le monde de la physique.
Nous espérons que vous ayez apprécié notre rapport autant que nous l’avons fait.
