Détermination d’un moment d’inertie

But : Déterminer le moment d’inertie d’un cylindre et comparer cette valeur expérimentale à la valeur théorique.

Méthode :

1. Peser deux cylindres ; un en laiton évidé et l’autre en aluminium plein.
2. Mesurer les dimensions de ces cylindres.
3. Mesurer la distance entre les deux cellules photoélectriques.
4. Mesurer l’inclinaison du plan.
5. Mesurer le temps mis par chaque cylindre pour franchir la distance entre les deux cellules pour différentes inclinaisons du plan.

Manipulations et mesures :

Distance entre les deux cellules photoélectriques : 0.998m ±0.001m

Cylindre de laiton
masse : 1.0620kg ±$1*10^{-4}kg$
diamètre extérieur : 0.05000m ±$5*10^{-5}m$
diamètre intérieur : 0.04010m ±$5*10^{-5}m$
longueur : 0.200m ±$1*10^{-3}m$

Cylindre d’aluminium
masse : 1.0613kg ±$1*10^{-4}kg$
diamètre extérieur : 0.05000m ±$5*10^{-5}m$
longueur : 0.200m ±$1*10^{-3}m$

Cylindre de laiton : L
Cylindre d’aluminium : A

Inclinaison en degrés, temps en secondes, tm : temps moyen.

Inclinaison	L t1	L t2	L t3	L tm	A t1	A t2	A t3	A tm
1.0	4.6	4.6	4.6	4.6	4.0	4.0	4.0	4.0
2.0	3.2	3.2	3.2	3.2	2.8	2.9	2.9	2.9
3.0	2.6	2.6	2.6	2.6	2.4	2.4	2.4	2.4
4.0	2.3	2.3	2.2	2.3	2.0	2.1	2.1	2.1
5.0	2.0	2.0	2.0	2.0	1.8	1.8	1.8	1.8

Calculs et graphiques :

– Masse volumique des cylindres :

Cylindre en laiton :

$\rho_{laiton}=\frac{m}{(\pi*r_{ext}^2- \pi*r_{int}^2)*h}$

$\rho_{minlaiton}=\frac{1.0619}{(\pi*0.025025^2-\pi*0.020025^2)*0.201}$
$\Rightarrow \rho_{minlaiton}=7465.74kg/m^3$

$\rho_{maxlaiton}=\frac{1.0621}{(\pi*0.024975^2- \pi*0.020075^2)*0.199}$
$\Rightarrow \rho_{maxlaiton}=7696.12kg/m^3$

$\rho_{laiton}=\frac{\rho_{maxlaiton}+\rho_{minlaiton}}{2}±\frac{\rho_{maxlaiton}-\rho_{minlaiton}}{2}$

$ \Rightarrow\rho_{laiton}=7580.93kg/m^3 ±115.19kg/m^3$

Cylindre en aluminium :

$\rho_{aluminium}=\frac{m}{\pi*r_{ext}^2*h}$

$\rho_{minaluminium}=\frac{1.0612}{\pi*0.025025^2*0.201}$
$\Rightarrow \rho_{minaluminium}=2683.51kg/m^3$

$\rho_{maxaluminium}=\frac{1.0614}{\pi*0.024975^2*0.199}$
$\Rightarrow \rho_{maxaluminium}=2721.86kg/m^3$

$\rho_{aluminium}=\frac{\rho_{maxaluminium}+\rho_{minaluminium}}{2}±\frac{\rho_{maxaluminium}-\rho_{minaluminium}}{2}$

$\Rightarrow\rho_{aluminium}=2702.69kg/m^3 ±19.18kg/m^3$

– Temps moyen de roulement pour chaque inclinaison :

$tm=\frac{t1+t2+t3}{3}$ (résultat dans le tableau ci-dessus)

– Accélération des cylindres pour les différentes inclinaisons :

$x=\frac{1}{2}at^2 \Rightarrow a=\frac{2x}{t^2}$ car la vitesse du cylindre au départ est nulle, et où x est la distance entre les deux cellules photoélectriques (0.998m ±0.001m) et t le temps de passage entre celles-ci.

$a_{min}=\frac{2x_{min}}{t^2}$
$a_{max}=\frac{2x_{max}}{t^2}$

$a=\frac{a_{max}+a_{min}}{2}±\frac{a_{max}-a_{min}}{2}$

Inclinaison en degrés, temps en $s$, a en $m/s^{2}$.
Cylindre de laiton : L
Cylindre d’aluminium : A

Inclinaison	L tm	L a min	L a max	L a
1.0	4.6	0.0942	0.0944	0.0943±0.0001
2.0	3.2	0.1947	0.1951	0.1949±0.0002
3.0	2.6	0.2950	0.2956	0.2953±0.0003
4.0	2.3	0.3769	0.3777	0.3773±0.0004
5.0	2.0	0.4985	0.4995	0.4990±0.0005

Inclinaison	A tm	A a min	A a max	A a
1.0	4.0	0.1246	0.1249	0.1248±0.0002
2.0	2.9	0.2371	0.2376	0.2374±0.0003
3.0	2.4	0.3462	0.3469	0.3466±0.0004
4.0	2.1	0.4522	0.4531	0.4527±0.0005
5.0	1.8	0.6154	0.6167	0.6161±0.0007

– Graphes de l’accélération des cylindre en fonction du sinus de l’angle d’inclinaison :

Cylindre en laiton :

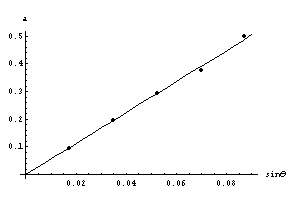
pente=5.61$m/s^{2}$

Cylindre en aluminium :

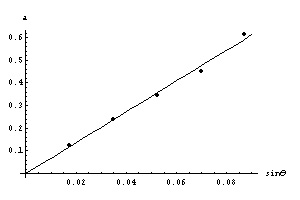
pente=6.81$m/s^{2}$

– Calcul des moments d’inertie des cylindres à partir des pente des graphiques :

On utilise l’équation qui exprime l’accélération du cylindre en fonction du moment d’inertie :

$a=\frac{mr^{2}gsin\theta}{mr^{2}+I}$

Où a est l’accélération du cylindre (égale à la pente du graphique), m sa masse, r son rayon, g l’accélération de la pesanteur et I son moment d’inertie.

En isolant le moment d’inertie on obtient :

$I=\frac{mr^{2}(g-a)}{a}$

$I=\frac{I_{min}+I_{max}}{2}±\frac{I_{max}-I_{min}}{2}$

Cylindre en laiton :

$I=\frac{\frac{1.0619*0.024975^{2}(9.81-5.61)}{5.61}+\frac{1.0621*0.025025^{2}(9.81-5.61)}{5.61}}{2}$
$±\frac{\frac{1.0621*0.025025^{2}(9.81-5.61)}{5.61}-\frac{1.0619*0.024975^{2}(9.81-5.61)}{5.61}}{2}$
$\Rightarrow I= 4.97*10^{-4}±1.04*10^{-6}kg*m^{2}$

Cylindre en aluminium :

$I=\frac{\frac{1.0612*0.024975^{2}(9.81-6.81)}{6.81}+\frac{1.0614*0.025025^{2}(9.81-6.81)}{6.81}}{2}$
$±\frac{\frac{1.0614*0.025025^{2}(9.81-6.81)}{6.81}-\frac{1.0612*0.024975^{2}(9.81-6.81)}{6.81}}{2}$
$\Rightarrow I= 2.92*10^{-4}±6.12*10^{-7}kg*m^{2}$

– Comparaison de ces résultats avec ceux obtenus avec les formules des tables CRM :

Cylindre en laiton :

$I=mr^{2} \Rightarrow I=1.0620*0.0225^{2} \Rightarrow I=5.38*10^{-4}kg*m^{2}$

$ (1-\frac{5.38*10^{-4}}{4.97*10^{-4}})*100=$-8.2%

Cylindre en aluminium :

$I=\frac{1}{2}mr^{2} \Rightarrow I=\frac{1}{2}*1.0613*0.025^{2} \Rightarrow I=3.32*10^{-4}kg*m^{2}$

$ (1-\frac{3.32*10^{-4}}{2.92*10^{-4}})*100=$-13.7%

Les moments d’inertie que nous avons obtenus expérimentalement sont inférieurs à ceux obtenus d’après les formules des tables CRM : de 8.2% pour le cylindre en laiton et de 13.7% pour celui en aluminium.

Conclusion :

Nous avons déterminé expérimentalement les moments d’inertie d’un cylindre creux en laiton et d’un plein en aluminium, respectivement de $5.38*10^{-4}kg*m^{2}$ et $3.32*10^{-4}kg*m^{2}$. Mais ils sont inférieurs de respectivement 8.2% et de 13.7% à ceux obtenus avec les formules des tables CRM, ce qui est en dehors de la marge d’incertitude de nos résultats. Cette dernière est donc sous-estimée. L’absence d’incertitude sur le temps de passage entre les deux cellules photoélectriques et l’inexactitude d’une vitesse de départ nulle pour les cylindres sont probablement les principales sources de ces résultats inférieurs aux valeurs théoriques.