Un parachutiste saute d’un avion. Après un certain temps, il ouvre son parachute puis se pose.
Le but de cette recherche est de trouver grâce à STELLA le moment le plus tard possible pour ouvrir son parachute afin d’arriver au sol avec une vitesse de 10 m/s.
Plan
1. Introduction
Lors d’un saut en parachute, la vitesse de chute est influencée par différentes forces :

- La force de pesanteur ou poids
P = m • g
| où m est la masse du parachutiste et g l’accélération gravitationnelle |
- La force de frottement
Ffrott = $\frac{1}{2}$ • ρ • Cx • S • v2
| où ρ représente la masse volumique de l’air, Cx est le coefficient de forme et S la surface apparente |
- L’accélération
a = $\frac{P-F_{frott}}{m}$
- La surface
S = π • r2
| où r est le rayon du parachute |
- Comme nous allons créer un modèle comportant une ouverture d’un parachute, ce qui signifie une augmentation brusque du rayon, nous allons utiliser dans STELLA les deux fonctions suivantes [1] :
$\circ$ STEP, qui crée une marche, un changement brusque.
$\circ$SMTH3, qui permet de lisser la fonction afin de la rendre plus réelle (l’ouverture du parachute prend un certain temps durant lequel le rayon augmente progressivement).
2. Données
Voici les données de base définissant des variables.
| la hauteur du saut | 1000 m |
| masse du parachutiste | 80 kg |
| vitesse lors du contact avec le sol | 10 m/s |
| rayon du parachutiste, parachute fermé | 0.75 m |
| rayon du parachutiste, parachute ouvert | 2 m |
| Cx | 1 |
| ρ | 1.293 kg/m3 |
| SMTHN | ⇒SMTH3 |
| Temps nécéssaire pour ouvrir le parachute | 3 sec |
| g | 9.81 m/s |
3. Modèle STELLA
Maintenant que nous avons posé les différentes formules ainsi que les données de base, nous pouvons créer le modèle suivant :
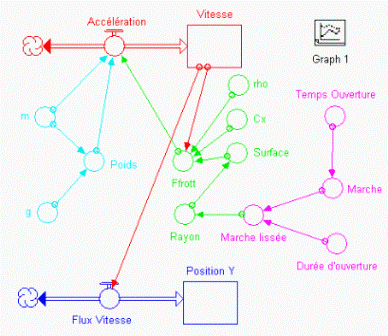
Nous remplissons le modèle avec les données suivantes [2] :

Nous lançons un graphique mettant en relation :
• La position Y
• La vitesse
en fonction du temps
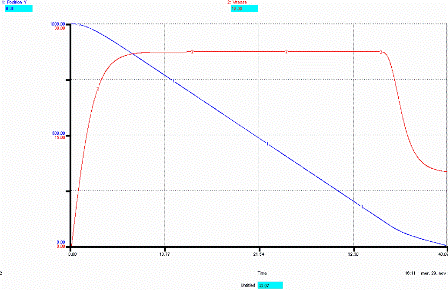
Afin d’être le plus précis possible, nous devons configurer le Run Spec comme suivant :
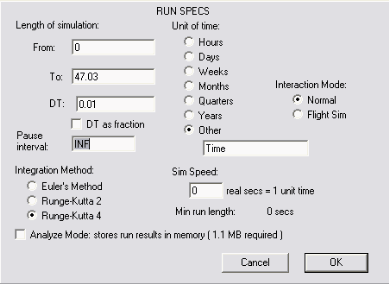
4. Conclusion
Nous voyons donc que le parachutiste doit ouvrir son parachute après 35.3 secondes pour arriver avec une vitesse de 10 m/s au sol.
Nous remarquons que pour un temps d’ouverture plus petit (<35.3 sec), le parachutiste arrivera aussi avec une vitesse de 9.83 m/s car le rayon de 2 m du parachute stabilise sa vitesse à 9.83 m/s.
Pour un temps d’ouverture plus grand (>35.3 sec), le parachutiste arrive avec une vitesse supérieure à 10 m/s(>10 m/s).
