Mesure de la période d’oscillation d’un pendule dans différentes situations.
– Introduction :
La notion d’oscillation, et celle de vibration qui lui est directement associée, est essentielle en physique. Le mouvement périodique est à la base de tout l’édifice théorique élaboré pour rendre compte de l’évolution temporelle quelconque d’un système. L’oscillateur a un comportement dépendant du temps. Il en existe plusieurs réalisations : la masse pesante suspendue à un ressort, le pendule et le diapason sont des exemples de systèmes au comportement périodique. L’oscillation qui nous interesse dans cette expérience est celle du pendule.
– But :
Mesurer la période d’oscillation T d’un pendule dans différentes situations, d’après cela, calculer g et en déduire différentes relations grâce à la théorie.
– Méthode et Mesures :
Mesurez la période d’oscillation T d’un pendule en fonction de sa longueur l
Masse : 50$g$
| Longueur en cm | Periode T en s |
| 76.8 | 1.7661 |
| 69.4 | 1.6949 |
| 65.8 | 1.6425 |
| 59.9 | 1.5734 |
| 53.3 | 1.4902 |
Mesurez la période d’oscillation d’un pendule de longueur fixe pour différentes masses et pour une amplitude inférieure à 20°
Longueur : 69.4$cm$
| Masse en g | Periode T en s |
| 50 | 1.6949 |
| 100 | 1.6605 |
| 150 | 1.6550 |
| 200 | 1.6482 |
| 250 | 1.6412 |
Mesurez la période du pendule pour des amplitudes variant de 10° à 90°
Longueur : 49.4$cm$
| Amplitude en ° | Periode T en s |
| 10 | 1.3828 |
| 20 | 1.3917 |
| 30 | 1.4051 |
| 40 | 1.4197 |
| 50 | 1.4485 |
| 60 | 1.4772 |
| 70 | 1.5235 |
| 80 | 1.5717 |
| 90 | 1.6352 |
– Questions :
- Graphique de $T$ en fonction de $\sqrt{l}$ :
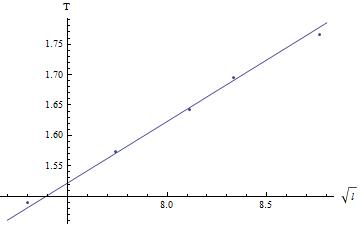
On remarque d’après le graphique que $T$ est proportionnel à $\sqrt{l}$.
- Pour calculer g, nous utiliserons la formule :
– $T=2\pi\sqrt{\frac{l}{g}}$
– $g=\frac{l}{{\left (\frac{T}{2\pi}\right)^2}}$
– $g=\frac{0.694}{{\left (\frac{1.6949}{2\pi}\right)^2}}=9.5374m/s^2$
Le $g$ théorique étant de $9.81m/s^2$, on remarque que le $g$ obtenu de nos mesures en est très proche.
- Graphique de $T$ en fonction de $m$.
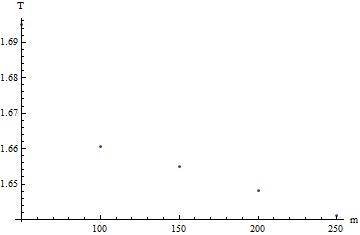
- Pour calculer la constante k d’un ressort afin qu’il oscille avec la même période lorsqu’on accroche chacune des masses utilisées à son extrémité libre nous utiliserons la formule suivante :
– $T=2\pi\sqrt{\frac{m}{k}}$
– $k=\frac{m}{{\left (\frac{T}{2\pi}\right)^2}}$
– $k=\frac{0.05}{{\left (\frac{1.6949}{2\pi}\right)^2}}=0.6871N/m$
- Graphique de $T$ en fonction de L’amplitude
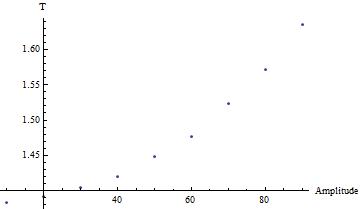
- On peut voir que plus l’amplitude est grande, plus la période sera grande. La théorie nous dit que $T$ dépend de l’amplitude et dans notre cas, cela se vérifie.
– Conclusion :
Dans cette expérience nous avons mesuré $T$ de diverses manières et déduit certaines choses :
- Nous remarquons que $T$ est proportionnel à $\sqrt{l}$.
- Nos mesures de $g$ ($9.5374m/s^2$) étaient très proches de la théorie ($9.81m/s^2$).
- Nous avons déterminé la constante $k$ (0.6871$N/m$).
- Nous avons déterminé que $T$ dépend de l’amplitude.
