Quels sont les nombres rationnels positifs x et y qui vérifient l’équation
x³+y³=9. Les solutions évidentes sont x=2, y=1 et x=1, y=2. Mais y en a-t-il d’autres ? Au XVII^e siècle, Pierre de Fermat mit au point une méthode géométrique efficace pour résoudre cette équation difficile de l’arithmétique. L’équation x³+y³=9 n’a pas seulement une interprétation algébrique. Elle définit aussi une courbe du plan, à savoir l’ensemble des points dont les coordonnées x et y vérifient l’équation x³+y³=9. Une droite quelconque d’équation y=ax+b coupe la courbe en, au plus, trois points distincts. Quand la droite est tangente à la courbe, le point de contact compte double. La méthode de Fermat repose sur le fait que si une droite est tangente à la courbe en un point de coordonnées rationnelles, et si elle coupe la courbe en un autre point, ce dernier a aussi des coordonnées rationnelles.

Lettre suivante

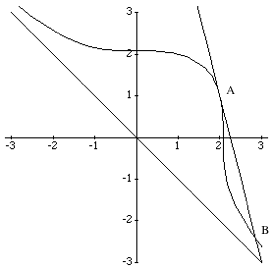
Voir aussi : Rational Points on an Elliptic Curve from The Wolfram Demonstrations Project.