Événements, représentation d’événements à l’aide des diagrammes d’espace-temps, intervalles, changement de référentiel, expressions des transformations.
par bernard.vuilleumier
Exercices sur les notions d’événements et d’intervalle entre deux événements. Représentation d’événements à l’aide des diagrammes d’espace-temps. Différentes expressions des transformations permettant de passer d’un référentiel à un autre.
Exercice 1
a) Un point a les coordonnées (2, 1) dans un système de référence. Quelles sont ses coordonnées dans un autre système qui a subi une rotation de $\frac{\pi}{3}$ par rapport au premier ?
– Rép. ($1+\frac{\sqrt3}{2}$, $\frac{1}{2}-\sqrt3$)
b) Un point a les coordonnées (4, 5) dans un système de référence qui a subi une rotation de $\frac{\pi}{5}$ par rapport au système d’origine. Quelles sont ses coordonnées dans le système d’origine ?
– Rép. (0.3, 6.4)
c) Vérifiez dans chaque cas qu’en appliquant la transformation inverse aux coordonnées obtenues, vous retrouvez les coordonnées de départ.
Exercice 2
1. Quatre événements (x, t) de coordonnées respectives (0, 0), (1, 0), (1, 1) et (0, 1) dans un système de référence $\Sigma$ sont observés depuis un système de référence $\Sigma$’ en translation rectiligne uniforme selon Ox à la vitesse v=15 m/s.
a) Donnez la transformation permettant de passer des coordonnées des événements exprimées dans $\Sigma$ aux coordonnées des événements exprimées dans $\Sigma$’.
b) Calculez les coordonnées de ces événements dans $\Sigma$’.
c) Dessinez ces événements dans $\Sigma$ et dans $\Sigma$’.
2. Les quatre événements (x, t) de coordonnées respectives (0, 0), (1, 0), (1, 1) et (0, 1) sont maintenant observés depuis un système de référence $\Sigma$’ en translation rectiligne uniforme selon Ox à la vitesse $\beta=\frac{1}{2}$.
a) Donnez la transformation permettant de passer des coordonnées des événements exprimées dans $\Sigma$ aux coordonnées des événements exprimées dans $\Sigma$’.
b) Calculez les coordonnées de ces événements dans $\Sigma$’.
c) Dessinez ces événements dans $\Sigma$ et dans $\Sigma$’.
Exercice 3
a) Représentez les événements ci-dessous à l’aide d’un diagramme d’espace-temps.
$E_1=(1, 0), E_2={\frac {\sqrt{26}}{5},\frac {1}{5}}, E_3=(\frac {\sqrt{29}}{5}, \frac{2}{5}),\ E_4=(\frac {\sqrt{5}}{2}, \frac{1}{2})$
$E_5=(\frac{\sqrt{34}}{5}, \frac {3}{5}), E_6=(\frac{\sqrt{41}}{5}, \frac{4}{5}),\ E_7=(\sqrt{2}, 1),\ E_8=(\frac{\sqrt{74}}{5}, \frac{7}{5})$
$E_9=(\frac {\sqrt{13}}{2}, \frac {3}{2})$
$E_{10}=(\frac {\sqrt{89}}{5}, \frac {8}{5})$
$E_{11}=(\frac {\sqrt{106}}{5}, \frac {9}{5})$
$E_{12}=(\sqrt{5}, 2)$
b) Calculez l’intervalle séparant chacun de ces événements de l’origine.
Exercice 4
1. Parmi les points de chacune des figures ci-dessous, quels sont ceux qui sont :
a) séparés par la même distance de l’origine O ?
b) séparés par le même intervalle de l’origine O ?
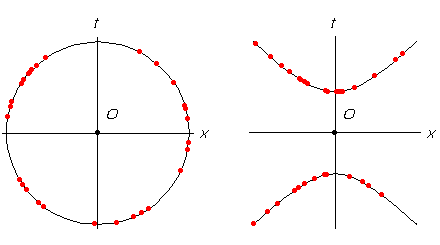
2. Y a-t-il des points, dans chacune de ces figures, qui sont séparés entre eux :
a) par une distance égale à celle qui les sépare de l’origine O ?
b) par un intervalle égal à celui qui les sépare de l’origine O ?
Exercice 5
Le passage d’un système de référence Σ à un autre &Sigma’ en translation uniforme selon Ox est donné par la transformation de Lorentz suivante :
a) Démontrez que cette expression de la transformation de Lorentz est équivalente à :
b) Donnez la relation entre β et θ.
c) Dessinez les systèmes de référence au moment où les origines coïncident :
- lorsque ${\theta}={\frac{\pi}{4}}$
- lorsque ${\theta}={\frac{\pi}{2}}$
d) Que vaut la vitesse relative de translation d’un système par rapport à l’autre pour chacune de ces valeurs de θ ?
e) Une règle de 1 m, placée sur l’axe Ox de Σ, est observée depuis Σ’. Quelle longueur l’observateur de Σ’ lui attribue-t-il ? Quelle longueur un observateur de Σ attribuerait-il à une règle de 1 m placée sur l’axe Ox’ de Σ’ ?
f) Deux événements A et B, se produisent au même endroit et sont séparés par un mètre de temps dans Σ. Quel temps s’écoule-t-il entre ces événements pour l’observateur de Σ’ ? Quel temps s’écoulerait-il entre ces événements se produisant au même endroit et séparés par un mètre de temps dans Σ’ pour un observateur de Σ ?
Exercice 6
a) Deux événements se passent au même endroit dans un système lié au laboratoire, mais sont séparés par une durée de trois secondes. Quelles sont les coordonnées de ces événements dans un système lié à un repère mobile si le rapport de la vitesse relative des systèmes à celle de la lumière vaut $\frac{1}{2}$ ?
b) Un méson π a une durée de vie propre (durée de vie dans le référentiel lié à la particule) de 2.55 10-8 s. Il se déplace à une vitesse égale au 12/13 de la vitesse de la lumière par rapport au laboratoire. Calculez la durée de vie de ce méson π dans le laboratoire.
Autres exercices
– sur le calcul d’erreur
– sur le mouvement
– sur les mouvements relatifs
– sur la relativité galiléenne
– sur les forces d’inertie
– sur la quantité de mouvement
– sur la gravitation
– sur l’énergie
– sur l’énergie relativiste
– sur les oscillations harmoniques
– sur l’énergie et les oscillations
– sur la rotation de solides rigides
– sur la notion de flux
– sur les grandeurs de l’électromagnétisme et leurs relations
– sur le mouvement de particules chargées dans un champ électrique
– sur l’induction et l’auto-induction
