
L’étude des systèmes dynamiques est une aire importante de la recherche actuelle en mathématiques et elle présente l’avantage d’être accessible au non spécialiste. Un aspect de cette étude fait intervenir l’itération de fonctions mathématiques. La question qui se pose est alors de savoir ce qui se produira si on itère encore et encore. Aussi surprenant que cela puisse paraître, même pour des expressions mathématiques très simples comme des fonctions quadratiques ou cubiques d’une variable réelle ou complexe, personne ne connaît la réponse complète ! Et il y a plusieurs mathématiciens de par le monde qui étudient très sérieusement cette question. C’est un exemple de problème actuel et irrésolu des mathématiques qu’il est facile d’exposer à des étudiants. Ils sont toujours très surpris d’apprendre que tout n’est pas encore connu à propos des fonctions quadratiques. Cela peut leur donner envie de se plonger dans cette étude et d’explorer par eux-mêmes.
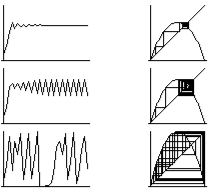
Evolutions conduisant à l’équilibre (première ligne), à un cycle périodique (deuxième ligne) ou au chaos (troisième ligne). Les graphiques de la première colonne donnent l’évolution temporelle, ceux de la deuxième illustrent la méthode graphique d’itération.
Voir aussi : Trajectories of the Logistic Map from the Wolfram Demonstrations Project.
