
Certaines transformations géométriques que l’on peut faire comprendre et illustrer facilement permettent d’obtenir des sous-ensembles « compliqués » d’espaces géométriques simples. Ces transformations peuvent agir sur différents espaces géométriques : droite, plan, etc. Un bon moyen de comprendre la signification des nombres exprimant la transformation d’un espace géométrique, consiste à examiner l’effet de cette transformation sur une figure, plutôt que sur un point de cet espace. On saisira ainsi mieux l’effet d’une transformation linéaire du plan – qui transforme toujours les lignes droites en lignes droites et qui peut être définie à l’aide de quatre nombres uniquement.
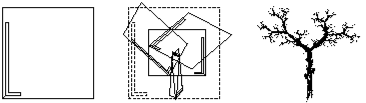
Voir aussi : Fractal Creation with Iterated Function Systems from the Wolfram Demonstrations Project.
